Note a cura di Roberto Bigoni
Un proiettile di massa m colpisce con velocità
v0 un bersaglio di massa infinita
perpendicolarmente alla sua superficie conficcandosi
completamente in esso.
Il proiettile si ferma perché nel suo moto nel 'fluido'
bersaglio è sottoposto ad una forza di attrito viscoso
f che, per velocità basse è, con buona
approssimazione, proporzionale alla velocità v.
![]()
La costante k dipende solo dalla forma della
pallina e dalla viscosità del bersaglio. Per il secondo principio
della dinamica
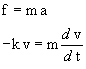
Questa è un'equazione differenziale che si risolve agevolmente separando le variabili:
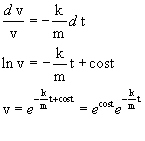
Ponendo come condizione iniziale v(0) =
v0, si ottiene
![]()
cioè la velocità, mentre la pallina si conficca nel bersaglio, decresce esponenzialmente fino ad annullarsi, teoricamente, per t che tende all'infinito.
Per capire quanta strada fa la pallina nell'argilla, si ricava x integrando v rispetto al tempo
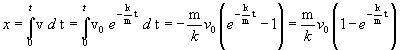
Calcolando il limite per t che tende all'infinito si ha in definitiva
![]()
Questo risultato rappresenta lo spostamento della pallina all'interno del bersaglio: a parità di k (quindi di viscosità del bersaglio e forma della pallina) è direttamente proporzionale alla quantità di moto del proiettile al momento dell'impatto con il bersaglio.
Noti Δx, m, v0 è possibile
calcolare k.
![]()
Ad esempio, se un proiettile di m = 10 g e
v0 = 500 m/s si conficca in un bersaglio
con una profondità Δx = 5 cm
![]()
Noto il valore di k si potrà calcolare la
profondità di penetrazione di un proiettile di ugual forma nello
stesso bersaglio per cui m = 20 g e
v0 = 400 m/s
![]()