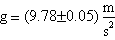Per effettuare la nostra valutazione dell'accelerazione di gravità locale ci siamo serviti del pendolo di Kater.
Quello a nostra disposizione era costituito da una massiccia sbarra di metallo su cui, a distanza di (1.000±0.003) m, erano posti due cunei uguali entrambi i quali potevano essere posti nella sede d'oscillazione del pendolo diventandone il fulcro. Lungo il tratto di sbarra compreso tra i due cunei si trovavano due masse mobili libere di scorrere lungo la sbarra ed essere fissate a qualsiasi altezza in modo da variare la posizione del baricentro del pendolo; oltre un fulcro era invece applicata la massa fissa.
Le masse mobili erano già state posizionate in modo tale ottenere lo stesso valore del periodo T indipendentemente da quale fosse il cuneo sul quale oscillava.
(Si veda teoria pendolo di Kater).
Abbiamo appoggiato un cuneo nella sede d'appoggio e abbiamo messo in movimento il pendolo in modo che compisse piccole oscillazioni e che l'estremità inferiore della sbarra attraversasse il raggio di luce emesso da una fotocellula posta ai suoi piedi. Poiché quest'ultima era stata precedentemente collegata ad un cronometro (sensibilità 0.001 s) ci è stato possibile valutare la durata del periodo di oscillazione. Dopo aver misurato la durata di venti periodi abbiamo capovolto il pendolo e ripetuto l'esperienza facendolo oscillare sull'altro coltello.
Sfruttando la relazione

una volta conosciuti T e d (dove d è la distanza tra i due fulcri) ci è stato possibile ottenere il valore di g.
I valori che abbiamo ottenuto dalla misurazione sono:
| T1 | T2 |
|---|---|
| 2009 | 2009 |
| 4019 | 4017 |
| 6028 | 6026 |
| 8037 | 8036 |
| 10046 | 10045 |
| 12054 | 12054 |
| 14063 | 14063 |
| 16072 | 16072 |
| 18081 | 18080 |
| 20090 | 20090 |
| 22100 | 22100 |
| 24110 | 24109 |
| 26118 | 26118 |
| 28127 | 28127 |
| 30136 | 30135 |
| 32144 | 32144 |
| 34154 | 34154 |
| 36162 | 36163 |
| 38170 | 38173 |
| 40180 | 40181 |
Ordinando i dati per frequenza si ottiene:
| T1 (s) | Frequenza |
| 2,008 | 5 |
| 2,009 | 10 |
| 2,010 | 5 |
| T2 (s) | Frequenza |
| 2,008 | 4 |
| 2,009 | 10 |
| 2,010 | 6 |
I periodi medi risultano quindi
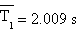
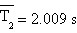
A tali valori associamo l'incertezza ΔT ottenuta con la deviazione standard della media moltiplicata per tre in modo da ottenere un intervallo in cui la probabilità che vi sia compreso il valore reale della misurazione sia del 99,7%:
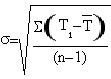
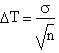
ΔT1=0.002 s e ΔT2=0.002 s
T1 (2.009±0.002) s T2 (2.009±0.002) s
Ovviamente i due valori coincidono perchè le masse sull'asta del pendolo erano state regolate in modo da ottenere questa condizione.
Ricordando la relazione sopracitata tra g ed il T d'oscillazione di un pendolo abbiamo ottenuto
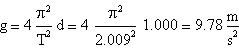
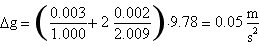
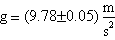
Per tentare di rendere minima l'incidenza degli errori sull'esperienza è stato necessario utilizzare alcuni accorgimenti.
Innanzitutto la massiccia sbarra di ci siamo serviti era di metallo rigido in modo tale da poterla considerare con buona approssimazione inestensibile.
Inoltre la cuneiformità dei fulcri ci ha permesso di valutarne la loro distanza reciproca con grande precisione poiché la punta del coltello è talmente sottile in rapporto alla lunghezza della sbarra (ovviamente ciò è tanto più vero quanto più la sbarra è lunga) da rendere minima l'incidenza dell'errore nella misurazione della sua posizione. Nel nostro caso però questo vantaggio è stato in parte vanificato dal metro di cui ci siamo serviti che non era ricavato da un'unica asta rigida graduata, ma era un metro pieghevole e quindi flessibile.
Grande importanza ha avuto poi l'utilizzo della fotocellula collegata al cronometro la cui precisione, basandosi su un sensore ottico, è estremamente migliore di quella ottenibile con l'utilizzo di un cronometro azionato manualmente che inevitabilmente risente del ritardo dei riflessi dell'osservatore.
Benché la nostra esperienza possa essere stata affetta da errori sfuggiti alla nostra attenzione o al nostro controllo come, ad esempio, l'attrito dell'aria che dovremmo considerare se avessimo la pretesa di valutare g con una sensibilità maggiore, e nonostante i risultati siano migliorabili con l'utilizzo di un pendolo più lungo sul quale gli errori incidono meno (a patto però di fornirgli una manutenzione costante poiché una sbarra più lunga, diventando molto pesante, usurerebbe rapidamente sia i fulcri sia le sedi d'appoggio) la nostra esperienza sembra aver fornito risultati verosimili.
Il valore di g che abbiamo ottenuto è infatti, come dalle nostre aspettative,uguale negli errori,benchè molto meno preciso, al suo valore medio ufficiale, fatto compatibile con la latitudine in cui si trova Bologna che è poco al di sotto del 45° parallelo passante per Genova (latitudine media tra l'Equatore ed il Polo Nord). Pur considerando tutti i limiti della nostra esperienza possiamo comunque affermare che il valore dell'accelerazione gravitazionale a Bologna è di circa