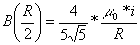è facilmente comprensibile dall'analisi della legge di Biot-Savart che un singolo conduttore attraversato da un corrente di media intensità (0.5 A) genera un campo di induzione magnetica talmente tenue da essere quasi ininfluente all' interno del campo magnetico terrestre (5*10 -5 Tesla). Di conseguenza, per ottenere campi magnetici "fruibili", sarà buona regola utilizzare strutture facilmente cumulabili e di "scarso ingombro".
Nel caso di una struttura come la spira sarà semplice costruire una bobina contenente un elevato numero di avvolgimenti ottenendo così un campo di induzione magnetica pari al prodotto del numero delle spire per il campo generato da ognuna di esse in un determinato punto. Inoltre, posizionando frontalmente due bobine percorse da una medesima corrente (intensità e verso), si otterrà un campo di induzione magnetica di valore doppio.
Tornando alla parte teorica sarà possibile dedurre il campo di induzione magnetica sull'asse di una spira ( forma circolare) partendo dalla, già citata, legge di La Place.
Considerando P situato sull'asse della spira per calcolare l'intensità del campo in quel punto è comodo considerare , astrattamente, due a due le frazioni di spira che la compongono.
In particolare sarà utile prendere in considerazione un punto ed il suo simmetrico rispetto all'asse. è facilmente deducibile (come si vede da figura) che l'unica componente efficace per ogni frazione di spira è soltanto quella verticale, in quanto, quella orizzontale risulta annullata "dal suo simmetrico". Inoltre, per dedurre il verso del campo, è sempre comoda la "legge della vite": se per l'osservatore la corrente circola in senso orario si troverà di fronte ad un campo entrante, "in allontanamento" da sè.

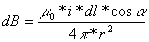
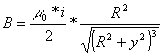
Nel caso specifico di un punto situato ad una distanza R/2 dal centro della spira(sempre sull'asse) B sarà: