Mathematica

Le sessioni di Mathematica si svolgono scrivendo e leggendo su uno o più notebook. Oltre al notebook che si apre per default al lancio del programma si possono aprire nuovi notebook tramite la funzione File->New del menù principale o caricare notebook precedentemente elaborati e salvati in opportune cartelle tramite la funzione File->Open del menù principale.

Può essere opportuno dotare il notebook attivo di una Toolbar (barra di pulsanti) per velocizzare le più comuni operazioni. A questo scopo attivare la funzione Format->Show ToolBar del menù principale.

Il nome di un nuovo notebook è provvisoriamente definito da Mathematica: ad esempio, come s'è detto, il nome del notebook attivo alla partenza del programma è "Untitled-1", come si può leggere nella prima riga a sfondo blu della finestra. Tale nome provvisorio permane fino a quando l'utente decide di salvare o di chiudere il notebook.

Per salvare un notebook cliccare sull'icona con il dischetto nella barra dei pulsanti oppure usare le funzioni File->Save e File->Save As del menù principale.

Per chiudere un notebook cliccare sul pulsante in alto a destra con la x (questo pulsante è standard in tutte le finestre di Windows).

Quando si si chiude o si salva un notebook che ha ancora un nome provvisorio, una apposita interfaccia chiede con che nome e in quale collocazione registrare il file. In previsione di ciò, è consigliabile predisporre da Windows una cartella per i propri notebook.

Un notebook è organizzato in blocchi segnalati da parentesi quadre visibili sulla destra della finestra . Ogni blocco può a sua volta segmentarsi in sottoblocchi.

Ad esempio: digitare '1'. Sul notebook compare '1' e sulla destra una parentesi quadra.

Premendo ora il tasto di Invio succede semplicemente che il cursore va a capo, perché i notebook di Mathematica possono limitarsi a contenere testi, come un normale editor, senza che sia necessaria una elaborazione specificamente matematica.

Se si vuole che l'input sia elaborato e venga prodotto un output bisogna premere il tasto di Shift (maiuscole) e, tenendolo premuto, premere anche Invio.

Dopo tale azione sullo schermo compaiono le seguenti scritte:

In[l]:=1
Out[l]=1

e sulla destra la parentesi di blocco si è espansa per contenere due sottoblocchi.

Cliccando doppio sulla parentesi più esterna il blocco si comprime fino a contenere solo

In[l]:=1

La risposta di Mathematica va interpretata in questo modo: l'utente ha sottoposto al programma il calcolo dell'espressione '1'. Il programma ha effettuato il calcolo producendo e visualizzando il valore di tale espressione.

Ovviamente il calcolo dell'espressione costituita dal singolo elemento numerico '1' non è molto interessante, ma con la stessa procedura si può calcolare il valore di espressioni più significative, contenenti molti tipi di operandi numerici e simbolici e molti tipi di operatori, organizzati in vari livelli di calcolo segnalati dalle parentesi algebriche (le tonde).

Sqrt[9]
Sin[3/4 Pi]
Sinh[Sqrt[2]]
(2+I)^2

Allo scopo di velocizzare e semplificare le operazioni di input Mathematica dispone di numerose serie di tavolozze contenenti gli schemi predefiniti di delle operazioni più usuali. Queste tavolozze (in inglese 'palette') possono essere selezionate nella funzione File->Palettes del menù. Gli schemi ('template') di uso più frequente si attivano con i sottomenù

Attivando uno di questi sottomenù viene visualizzata nella parte destra dello schermo la tavolozza corrispondente. Ad esempio

Espandere eventualmente la lista degli oggetti che interessano cliccando sul triangolino di fianco al nome della lista e cliccare poi sul simbolo dello schema voluto. Si ottiene così la riproduzione dello schema nel notebook. Nello schema compaiono campi in cui inserire i dati direttamente da tastiera o da altri simboli della tavolozza, come, ad esempio, nel caso si voglia scrivere la radice quadrata di una potenza. Per passare da un campo all'altro di uno schema conviene usare il tasto di tabulazione.

Help.

La caratteristiche più interessanti di Mathematica sono fondamentalmente le seguenti:

Per evitare errori e perdite di tempo per la loro correzione va ribadito che tutti gli operatori, tutte le funzioni e tutte le costanti 'built in' hanno sempre l'iniziale maiuscola (e bisogna fare attenzione, perché Mathematica è 'case sensitive', cioè distingue tra maiuscole e minuscole) e gli argomenti delle funzioni e degli operatori vanno sempre tra parentesi quadre.

Il repertorio di tutti i tipi di elaborazione effettuabili con Mathematica è sempre consultabile attivando la funzione Help del menù.

Si apre un menù a tendina nel quale la funzione più importante è Help Browser.

Attivando questa funzione compare un'interfaccia di uso intuitivo che permette di accedere alla documentazione su operatori, funzioni e procedure di vario tipo, illustrando il loro significato, il modo di usarli, collegamenti a funzioni correlate e fornendo esempi concreti.

Si provi cercando in Help la documentazione su simboli di uso frequente come Cos, Sin, Pi.

L'aritmetica

Il modo più semplice di lavorare con Mathematica è di usarlo come una supercalcolatrice, in grado di svolgere calcolo numerico esatto ed approssimato a qualunque grado di precisione richiesto dall'utente.

Il calcolo sugli interi è sempre esatto e completo, a differenza di quanto avviene nelle calcolatrici tascabili che per interi molto grandi passano forzatamente alla notazione esponenziale con mantissa approssimata.

123456789*234567890
100!
123456789^100
Quotient[111111111111111111111111,1111111111111]
Mod[111111111111111111111111,1111111111111]
GCD[123456,234567,345678]
LCM[123456,234567,345678]
Binomial[100,57]

Negli ultimi cinque esempi si sono usati operatori sugli interi (cercare la relativa documentazione in Help):

Divisors[3333333333333333]
FactorInteger[3333333333333333]
PrimeQ[5882353]
Prime[21]

(Le parentesi graffa non compaiono sulla tastiera italiana : per ottenerle premere contemporaneamente 'AltGr', 'Shift' e tasto delle quadre, oppure 'Alt' e le sequenze 123, 125 dal tastierino numerico.)

Table[Prime[i],{i,100}]
Table[Prime[i],{i, 1000,1100}]

Il primo comando produce la lista dei primi 100 numeri primi;
il secondo produce la lista dei numeri primi dal millesimo al millecentesimo.

Notare la sintassi: l'argomento di Table (consultare Help) è costituito da due oggetti: una espressione contenente una o più variabile e una o più liste il cui primo elemento è la variabile che può essere seguita o dall'ultimo valore assumibile (il primo è di default 1) o dal primo e ultimo valore assumibili. In questo modo la variabile i (che in questo caso è un semplice contatore) viene incrementata di una unità ad ogni passo.

Provare a costruire una lista di coefficienti binomiali.

Provare il seguente Input:
Table[ij,{i,10},{j,10}]

Provare a costruire le prime dieci righe del Triangolo di Pascal (o Tartaglia).

L'operatore % indica l'ultimo Output; %% indica il penultimo Output; %n indica l'ennesimo Output prodotto.

L'Output di MatrixForm può essere meglio organizzato usando l'opzione TableSpacing nel seguente modo:
MatrixForm[%,TableSpacing->{0,0}].

Le opzioni sono seguite da una freccetta realizzata unendo il tratto con il segno di maggiore.

Osservare l'effetto cambiando i valori nella lista di TableSpacing e consultare Help per tale voce.

Un altro interessante operatore sugli interi (ma anche sui razionali) è BaseForm, che produce la stampa di un numero decimale in un'altra base (max 36).

BaseForm[64,2]
BaseForm[1000000,16]
BaseForm[1000000,21]

Mathematica produce sempre il risultato esatto di una espressione e fornisce una approssimazione decimale solo se espressamente richiesta.

In generale operando su interi e frazioni, si ottengono frazioni ridotte ai minimi termini.

Il numero di cifre da visualizzare dopo la virgola può essere indicato come secondo argomento di N.

Produrre una progressione aritmetica di 10 termini con primo termine 1/2 e ragione 1/3 (usare Table).

Produrre una progressione geometrica di 10 termini con primo termine 1/2 e ragione 1/3.

Anche il calcolo di espressioni contenenti irrazionali è sempre matematicamente esatto.

Come si vede, gli irrazionali sono indicati simbolicamente con radicali, logaritmi o in generale come valori di funzioni algebriche o trascendenti, dirette o inverse, di argomenti razionali.

I valori di pi greco e del numero di Nepero sono indicati simbolicamente. Ad esempio, calcolando l'espressione

Per ottenere approssimazioni decimali, usare l'operatore N come descritto sopra.

N[Pi]
N[Pi,200]
N[Pi/2,100]
N[Pi/3,20]
N[Pi^E]
N[GoldenRatio,100]
Log[E]
Log[E,10]

Le approssimazioni dei numeri reali oltre che in virgola fissa possono essere denotate in virgola mobile moltiplicando la mantissa per una potenza di dieci.

Gli argomenti delle funzioni trigonometriche si intendono sempre in radianti.

Nel caso li si voglia esprimere in gradi sessagesimali vanno moltiplicati per la costante predefinita Degree.

Sin[30 Degree]
Cos[45 Degree]
Tan[60 Degree]

Ottenere in gradi il valore delle seguenti funzioni inverse:
ArcoSeno di 1
ArcoCoseno di 1/2
ArcoTangente di 1

Equazioni e sistemi.

L'operatore Solve permette di risolvere equazioni e sistemi. Solve richiede due argomenti: una equazione (o una lista di equazioni) e una variabile (o una lista di variabili).

Notare che il segno di uguaglianza in Mathematica va indicato (come in C e Java) raddoppiando l'usuale segno algebrico.

Solve[x^2-4==0,x]
Solve[x^4-2x^3-3x^2+8x-4==0,x]
Solve[Cos[x]==Sqrt[3]/2,x]
Solve[{x+y==3,x-y==l},{x,y}]

Solve funziona egregiamente quando sia possibile ottenere le soluzioni in forma esatta usando radicali e funzioni inverse.

Negli stessi casi si possono ottenere direttamente le approssimazioni decimali delle soluzioni usando NSolve.

NSolve[Cos[x]==Sqrt[3]/2,x]

Quando non è possibile ottenere soluzioni esatte, bisogna usare FindRoot che cerca soluzioni approssimate con algoritmi iterativi come quello di Newton o quello delle secanti.

FindRoot[Cos[x]==x,{x,l/2}]

Nella ricerca degli zeri di una funzione reale di variabile reale e più in generale nello studio di una funzione può risultare utile tabulare la funzione in un intervallo preassegnato o graficarla.

Per ottenere una tabella di una funzione si può usare Table nella sua sintassi completa: la lista che inizia con la variabile comprende oltre ad essa altri tre termini: il valore iniziale, quello finale e l'incremento.

Table[{x,Sin[x]},{x,-Pi,Pi,Pi/10}]

ColumnForm[Table[{x,Sin[x]},{x,-Pi,Pi,Pi/10}]]

Algebra

Mathematica può svolgere molte delle più comuni operazioni di elaborazione algebrica su espressioni letterali.

Gli operatori più importanti nelle operazioni su polinomi sono Expand e Factor che realizzano lo sviluppo e la fattorizzazione di un polinomio.

Expand[(a+b)^3]
Expand[(x^2-x+3)(x-2)]
Factor[%]
Factor[a^2-b^2]
Factor[a^3-b^3]

Simplify[(a^3+b^3)/(a+b)]

Gli operatori Together e Apart operano inversamente uno dall'altro: il primo somma frazioni; il secondo tenta di scrivere una frazione come somma di frazioni di denominatore di grado minore possibile.

Together[l/(a-b)+l/(a+b)]
Apart[%]

(Attenti a staccare bene la 'a' dalla 'x': 'a' staccato da 'x' rappresenta il prodotto a per x ; ax è un unico simbolo!).

Grafica 2D

Per visualizzare il grafico di una funzione di una variabile reale nel piano xOy usare l'operatore Plot.

Nella sintassi più semplice di Plot l'argomento è composto da una funzione e da una lista (tra graffe) comprendente 3 elementi: la variabile della funzione e gli estremi dell'intervallo di variabilità.

Plot[Sin[x],{x,-2Pi,2Pi}]

Cliccando in un punto interno al grafico compare il contorno rettangolare del grafico. Trascinando il mouse, il grafico si sposta nella posizione ritenuta più adeguata. Cliccando su uno dei quadratini neri situati nei vertici e nei punti medi dei lati del contorno e trascinando il mouse si variano le dimensioni del grafico.

Gli assi non sono monometrici, ma le unità di misura sono scalate in modo da permettere la miglior rappresentazione della funzione dell'intervallo richiesto.

Per default il grafico viene prodotto in un riquadro rettangolare le cui dimensioni sono in proporzione aurea. Se si vuole il grafico in un quadrato, usare l'opzione AspectRatio con valore 1:

Plot[Sin[x],{x,-2Pi,2Pi},AspectRatio->l]

Titolo del grafico e variabili sugli assi si indicano con le opzioni PlotLabel e AxesLabel:

Plot[Sin[x],{x,-2Pi,2Pi},PlotLabel->"Grafico del Seno", AxesLabel->{"x","Sen x"}]

Plot[Sin[x^2],{x,-Pi,Pi}Frame->True,FrameLabel->"Sen x^2"]

Se un grafico ha singolarità o estremi molto pronunciati si può ottenere una rappresentazione più chiara limitandone l'estensione verticale con l'opzione PlotRange determinata da una lista di due valori indicanti il massimo e minimo graficabile.

Plot[Tan[x],{x,-2Pi,2Pi},PlotRange->{-8,8}]
Plot[Log[x],{x,1/1000,1000},PlotRange->{-2,2}]

Produrre il grafico della parabola y=x².
Produrre il grafico della parabola y=4-x².
Produrre il grafico di iperboli equilatere con asintoti sugli assi.

Si possono produrre i diagrammi di più curve sullo stesso grafico, mettendo le funzioni in una lista come primo argomento di Plot.

Plot[{Sin[x],Cos[x]},{x,-Pi,Pi}]

Plot[Evaluate[Table[x+k,{k,-3,3}],{x,-4,4}]]

Graficare un fascio di rette con centro nell'origine.
Graficare un fascio di parabole con il vertice nell'origine.

Una volta prodotto un oggetto grafico, lo si può visualizzare ed eventualmente modificare con Show.

Show è un operatore il cui primo argomento deve essere un oggetto grafico eventualmente seguito dalle opzioni di visualizzazione.

Show[Plot[Evaluate[Table[x+k,{k,-3,3}],{x,-4,4}]],Frame->True]

Dichiarazione di oggetti costanti. Altra Grafica 2D

Usando Show si possono visualizzare altri elementi grafici come punti, segmenti, cerchi, rettangoli, poligoni.

In casi del genere conviene però indicare tali elementi con un opportuno identificatore deciso dall'utente.

L'assegnazione di un valore costante ad un identificatore si fa con il segno di uguaglianza '='.

Ad esempio, la visualizzazione dei punti {0,0},{1,1},{2,0},{3,1},{4,0} si ottiene con ListPlot.

lista={{0,0},{l,l},{2,0},{3,1},{4,0}}
ListPlot[lista,PlotJoined->True]

La poligonale che unisce i punti {0,0},{1,1},{2,0},{3,1 },{4,0} si può ottenere anche con l'operatore Line che ha come argomento la lista delle coppie.

lista={{0,0},{l,l},{2,0},{3,1},{4,0}}
linea=Graphics[Line[lista]]
Show[linea,Frame->True]

Per disegnare una circonferenza si usa l'operatore Circle che richiede come argomento la coppie di coordinate che individua il centro e il raggio:

circonferenza=Graphics[Circle[{0,0},4]]
Show[circonferenza,Frame->True,FrameLabel->"circonferenza"]

Show[{linea,circonferenza},Frame->True,FrameLabel->"circonferenza e poligonale"]

parabola=Plot[x^2,{x,-4,4}]
Show[{parabola,circonferenza},Frame->True,FrameLabel->"circonferenza e parabola"]

L'associazione di un oggetto ad un identificatore, anche se non indispensabile, facilita molto l'elaborazione. Per esempio può essere comodo un identificatore per la metà o il doppio di pi greco (evitare di usare le iniziali maiuscole):

pimezzi = Pi/2
duepi = 2Pi

g=9.81
gr=6.67 10^(-11)
me=9.11 10^(-31)

Date in unità S.I. la massa della Terra mt=5.98 10^24 e il suo raggio medio rt=6.67 10^6, calcolare la densità media e la velocità di fuga.

Dichiarazione di funzioni.

In aggiunta alle funzioni di libreria (built in) l'utente può definire nuove funzioni utili alle sue applicazioni.

L'intestazione si compone di un identificatore seguito da una coppia di quadre contenenti i simboli alfanumerici di una o più variabili indipendenti: se più di una, separarle con virgole. Nell'intestazione i simboli delle variabili indipendenti devono terminare con il tratto di sottolineatura _.

Per le più usuali funzioni algebriche il corpo della funzione è descritto da un'espressione nella quale le variabili elencate nell'intestazione vanno riportate senza il carattere di sottolineatura finale.

L'associazione del corpo all'intestazione viene indicata dalla sequenza := (come in Pascal).

Quando si è definita una funzione, la si può utilizzare come quelle di libreria per calcolarne valori specifici, per tabularla, per graficarla, per risolvere equazioni, per definire altre funzioni.

quadrato[x_] := x*x
ColumnForm[Table[{x,quadrato[x]},{x,0,10}]]
Plot[quadrato[x],{x,-3,3}]
Solve[quadrato[x]==10,x]
NSolve[quadrato[x]==10,x]
f1[x_] := quadrato[Sin[x]]-1/2 Cos[x]
Plot[f1[x],{x,-2Pi,2Pi}]
FindRoot[f1[x]==0,{x,0,2}]

Le funzioni possono essere ricorsive, cioè nel loro corpo possono richiamare la funzione stessa. Ovviamente in casi del genere è necessario che la definizione della funzione contenga una condizione di uscita dal ciclo di ricorsione.

fattoriale[0]=1
fattoriale[n_] := n*fattoriale[n-l]

Notare la differenza tra le assegnazioni nei due casi: nella prima assegnazione si stabilisce un preciso valore 1 in corrispondenza dell'argomento O; nella seconda è definito il calcolo in corrispondenza di un generico argomento n.

Produrre la stampa dei primi dieci termini della successione di Fibonacci.
(La successione di Fibonacci ha come primi termini 1 e 1; ogni altro termine è dato dalla somma dei due precedenti.)

Verificare che il rapporto tra ogni numero di Fibonacci e il precedente tende al rapporto aureo.

Funzioni più articolate e interessanti per l'analisi si possono ottenere con l'uso dell'operatore If.

If ha solitamente tre argomenti: il primo è la condizione, il secondo specifica l'azione nel caso di verità della condizione, il terzo l'azione in caso di falsità (la struttura è fondamentalmente quella dell' if...then...else dei linguaggi di programmazione).

f1[x_] := If[x<0,1+x,1-x]
Plot[f1[x]],{x,-2,2}]

Un costrutto di questo genere diventa indispensabile, ad esempio, con i radicali.

Poiché le radici vanno espresse come potenze di esponente frazionario e tali potenze sono legittime solo per basi positive, una radice cubica va definita in questo modo:

rad3[x_] := If[x>=0,x^(1/3),-(-x)^(1/3)]

Derivate e integrali.

Il modo più semplice per ottenere la funzione derivata prima di una funzione di una variabile reale (di libreria o dichiarata dall'utente) è quello di far seguire l'identificatore della funzione da un apice.

Sin'[x]
Tan'[x]
(dichiarazione della funzione f1)
f1[x_]:=x^3+x^2+x+1
(derivazione della funzione f1)
f1'[x]
(dichiarazione della funzione f2)
f2[x_]:=(x^2-1)/(x^2+1)
(semplificazione della derivata di f2)
Simplify[f2'[x]]
(definizione della funzione df2, derivata di f2)
df2[x_]:=f2'[x]

Per avere la derivata seconda, terza, ecc. duplicare o triplicare il numero di apici.

Sin''[x]
Simplify[Tan'''[x]]
(dichiarazione della funzione f1)
f1[x_]:=x^3+x^2+x+1
(derivata seconda della funzione f1)
f1''[x]

Alternativamente si può usare l'operatore Dt (derivata totale) con argomenti dati dalla funzione da derivare e dalla variabile rispetto alla quale derivare, se si vuole la derivata prima, oppure una coppia costituita dalla variabile e dall'ordine di derivazione.

Dt[Sin[x],x]
Dt[Sin[x],{x,2}]
(dichiarazione della funzione f1)
f1[x_]:=x^3+x^2+x+1
(derivata terza della funzione f1)
Dt[f1[x],{x,3}]

L'operatore Dt con argomento costituito dalla sola funzione restituisce il differenziale totale della funzione.

Per ottenere l'integrale indefinito di una funzione si usa l'operatore Integrate con argomenti dati dalla funzione da integrare e dalla variabile rispetto alla quale integrare. Gli integrali indefiniti prodotti da Mathematica non riportano la costante additiva indeterminata.

Integrate[Sin[x],x]
Integrate[Log[x],x]
(dichiarazione della funzione f1)
f1[x_]:=x^3+x^2+x+1
(integrazione della funzione f1)
Integrate[f1[x],x]

L'impostazione del calcolo degli integrali definiti segue una sintassi abbastanza simile a quella dell'integrazione indefinita ma la variabile di integrazione è compresa in una lista costituita dalla variabile stessa e dagli estremi di integrazione.

Integrate[Sin[x],{x,0,Pi}]
Integrate[Log[x],{x,1,E}]
(dichiarazione della funzione f1)
f1[x_]:=x^3+x^2+x+1
(integrazione della funzione f1)
Integrate[f1[x],{x,-3,3}]

Le operazioni di integrazione e di derivazione sono facilitate dall'uso della tavolozza di Mathematica qui riprodotta.

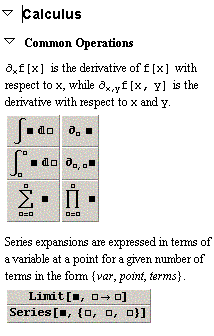
Nella tavolozza sono mostrate anche le sintassi per ottenere limiti e sviluppi in serie.

Per ottenere limiti e sviluppi in serie scrivendo gli input da tastiera vedere i seguenti esempi:

Limit[Sin[x]/x,x->0]
Series[Log[1+x],{x,0,10}]

Le icone con Σ e Π della tavolozza scrivono sul notebook gli schemi per il calcolo di sommatorie e prodotti: la loro sintassi in linea è desumibile dai seguenti esempi

(per ottenere la somma dei quadrati dei numeri naturali da 1 a 10)
Sum[i^2,{i,10}]
(per ottenere la somma dei quadrati dei numeri naturali da 10 a 20)
Sum[i^2,{i,10,20}]
(per ottenere la somma dei quadrati dei numeri pari da 2 a 10)
Sum[i^2,{i,2,10,2}]
(per ottenere il prodotto dei quadrati dei numeri naturali da 1 a 10)
Product[i^2,{i,10}]
(per ottenere il prodotto dei quadrati dei numeri naturali da 10 a 20)
Product[i^2,{i,10,20}]
(per ottenere il prodotto dei quadrati dei numeri pari da 2 a 10)
Product[i^2,{i,2,10,2}]

Vettori e matrici.

Vettori di uguali dimensioni possono essere addizionati e sottratti, moltiplicati scalarmente e vettorialmente. Somma e sottrazione si ottengono con gli usuali segni, il prodotto scalare si ottiene con l'operatore Dot, il prodotto vettoriale si ottiene con l'operatore Cross.

v1={1,2,3}
v2={1,-1,1}
2v1
v1+v2
v1-v2
Dot[v1,v2]
Cross[v1,v2]

La dimensione di un vettore (e in generale la lunghezza di una lista) è prodotta dall'operatore Length. Le componenti di un vettore (e più in generale gli elementi di una lista) possono essere individuate facendo seguire il nome del vettore da una doppia coppia di parentesi quadre contenente l'indice della componente.

v1={1,2,3}
v2={1,-1,1}
modulo[v_]:=Sqrt[Sum[v[[i]]^2,{i,1,Length[v]}]]
cosxy[x_,y_] := Dot[x,y]/(modulo[x]*modulo[y])
cosv1v2 = cosxy[v1,v2]
angv1v2 = N[ArcCos[cosv1v2]]/Degree

Una matrice quadrata di ordine n può essere moltiplicata scalarmente per un vettore dello stesso ordine. Due matrici quadrate dello stesso ordine possono essere sommate e moltiplicate tra loro. Di una matrice si può calcolare il determinante con l'operatore Det. Una matrice con determinante non nullo può essere invertita con l'operatore Inverse. Di una matrice quadrata si possono ottenere autovalori e autovettori con gli operatori Eigenvalues e Eigenvectors.

v1={1,2,3}
m1 = {{1, 2, 3}, {1, 1, -1}, {2, 0, 2}}
MatrixForm[m1]
Dot[m1,v1]
Det[m1]
invm1 = Inverse[m1]
Dot[m1,invm1]
m2 = {{1, 1, 0}, {-1, 2, 3}, {3, 2, -1}}
Det[m2]
Dot[m1,m2]
Eigenvalues[m1]
Eigenvectors[m1]

NOTE SULL'USO DI MATHEMATICA

Input e Output.