Quesito 1

Due lunghi fili rettilinei paralleli distanti d=8cm sono percorsi da correnti di verso opposto entrambe di intensità I=100A. Detto α un piano perpendicolare ai due fili, detti P e Q i punti in cui i fili intersecano α e detto O il punto medio del segmento PQ

1. calcolare l'intensità della forza che agisce su ogni metro di filo;
2. calcolare l'intensità di B in O;
3. calcolare l'intensità di B in un punto S di α, posto sull'asse del segmento PQ e distante y=3cm da O.

Svolgimento

Quesito 2

Una spira circolare conduttrice di sezione costante, centro O e raggio R=4cm, è posta nel vuoto.

1. Quale corrente I₀ deve circolare nella spira se si vuole che il modulo dell'induzione magnetica in O sia B₀=10^-4T?
2. Quale risulta, nel caso calcolato, il modulo B_R dell'induzione magnetica nei punti dell'asse della spira situati a distanza R da O?
3. A quale distanza D da O si trovano i punti del suo asse in cui il modulo di B è la metà di B₀?
4. Scelto un sistema di riferimento con origine in O e asse z coincidente con l'asse delle spira, quanto vale il modulo dell'integrale calcolato sull'asse della spira partendo da O fino a distanza infinita?

Svolgimento

Svolgimento del quesito 1

1. La forza per unità di lunghezza è data in modulo da

   

2. Nel punto O i contributi all'induzione magnetica totale dovuti alle due correnti, calcolabili con la legge di Biot-Savart, sono equiversi e di uguale intensità. Per ottenere il modulo dell'induzione risultante basta raddoppiare uno di questi contributi:

   

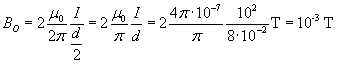
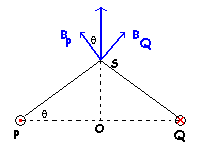
3. Il punto S dista 5 cm da entrambi i fili. I contributi all'induzione magnetica totale da parte delle due correnti sono uguali in modulo ma diversamente orientati. Le loro componenti perpendicolari all'asse OS sono opposte, quindi il campo di induzione risultante è dato dalla somma delle loro componenti secondo l'asse OS.
   Per ottenere l'intensità di tali componenti bisogna moltiplicare l'intensità ottenuta con la legge di Biot-Savart per il coseno dell'angolo θ che risulta 4/5.

   

Svolgimento del quesito 2

1. B₀ in funzione del raggio R e della corrente I₀ è data da

   

   quindi

   

2. In un punto dell'asse a distanza z da O il modulo di B è

   

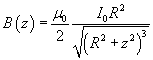
   Si ha quindi

   

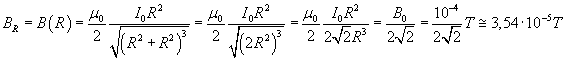
3. Bisogna risolvere l'equazione

   

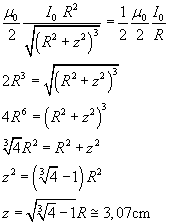
4. Ipotizzando per l'induzione B un percorso di circuitazione quadrato con un lato coincidente con l'asse della spira e i rimanenti tre lati a distanza infinita dalla spira, l'integrale indicato è, in modulo, la metà della circuitazione, cioè