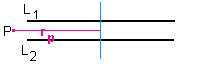
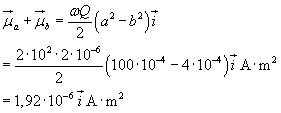 Due lastre conduttrici circolari parallele e coassiali L1 e L2,
entrambe di raggio R=1,00 m, sono poste nel vuoto a distanza d=8,85 cm l'una dall'altra.
Tra di esse viene instaurata una differenza di potenziale variabile nel tempo
Due lastre conduttrici circolari parallele e coassiali L1 e L2,
entrambe di raggio R=1,00 m, sono poste nel vuoto a distanza d=8,85 cm l'una dall'altra.
Tra di esse viene instaurata una differenza di potenziale variabile nel tempo
problema 1
 Due lastre conduttrici circolari parallele e coassiali L1 e L2,
entrambe di raggio R=1,00 m, sono poste nel vuoto a distanza d=8,85 cm l'una dall'altra.
Tra di esse viene instaurata una differenza di potenziale variabile nel tempo
Due lastre conduttrici circolari parallele e coassiali L1 e L2,
entrambe di raggio R=1,00 m, sono poste nel vuoto a distanza d=8,85 cm l'una dall'altra.
Tra di esse viene instaurata una differenza di potenziale variabile nel tempo
![]() ,
con V0=1000 V e ω=100 s-1.
,
con V0=1000 V e ω=100 s-1.
Considerando trascurabili gli effetti di bordo, esprimere in funzione del tempo:
soluzione
Tra le due lastre c'è un campo elettrico di intensità
![]() perpendicolare alle lastre stesse.
perpendicolare alle lastre stesse.
La densità della corrente di spostamento risulta quindi
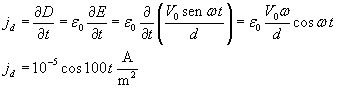
Scegliendo un percorso di circuitazione circolare di raggio rp delimitante una circonferenza il cui piano sia compreso tra i piani delle lastre, dalle equazioni di Maxwell si ha
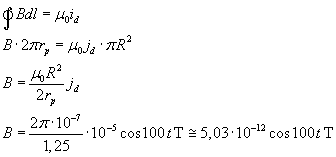
In particolare, se t=0,
![]()
problema 2
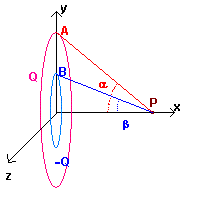 Due anelli filiformi, circolari e concentrici, giacciono nel piano [y , z] di figura.
Sull'anello esterno, avente raggio a= 10 cm, viene distribuita, uniformemente,
una carica Q=2μC e su quello interno (raggio b=2 cm) una carica -Q
Due anelli filiformi, circolari e concentrici, giacciono nel piano [y , z] di figura.
Sull'anello esterno, avente raggio a= 10 cm, viene distribuita, uniformemente,
una carica Q=2μC e su quello interno (raggio b=2 cm) una carica -Q
1) Si determini il campo elettrico nel punto P dell'asse x, di ascissa p=50 cm.
Si ponga ora una particella puntiforme, avente carica q=1 pC e massa m=10-3 g nel punto P.
2) Determinare qual è l'energia potenziale elettrica che possiede tale carica, supponendo che essa venga mantenuta ferma in P.
Trascurando gli effetti gravitazionali e considerando il tutto immerso nel vuoto, si lasci la particella libera di muoversi.
3) Si determini la velocità della particella quando essa transiterà, per la prima volta, dal centro O dei due anelli.
Si trascuri ora la presenza della carica q e si supponga che i due anelli vengano posti in
rotazione, con velocità angolare costante
![]() con ω=200 rad/s.
con ω=200 rad/s.
4) Si determini, in tale situazione, il momento di dipolo magnetico totale associato ai due anelli.
soluzione
Se si considera la carica infinitesima dq contenuta in un tratto infinitesimo dl dell'anello maggiore, il campo da essa determinato nel punto P risulta
![]()
dove il versore ur è quello del vettore da dq a P.
Dato che la carica simmetrica rispetto al centro produce in P un campo analogo ma con componente y opposta, di questo campo è efficace solo la componente x che si ottiene moltiplicando il modulo per il coseno di α (rapporto tra ascissa e distanza). Il campo efficace determinato da dq in P è quindi
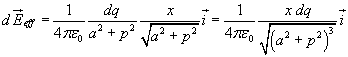
Il campo prodotto in P da tutto l'anello esterno si ottiene integrando, cioè in pratica sommando tutti gli elementi di carica dq ottenendo la carica totale Q.
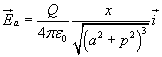
In modo analogo si ottiene il campo prodotto in P dall'anello interno che risulta
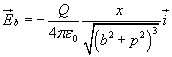
In definitiva il campo totale in P è quindi
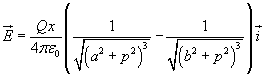
Eseguendo i calcoli si ottiene
![]()
Il potenziale prodotto in P da un elemento di carica dq sull'anello esterno risulta
![]()
e il potenziale prodotto da tutto l'anello è quindi
![]()
Analogamente per l'anello interno si ha
![]()
Il potenziale complessivo dei due anelli è quindi
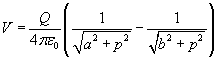
Calcolando si ottiene
![]()
L'energia potenziale è data da prodotto del potenziale per la carica
![]()
Il potenziale della particella nel centro degli anelli si ottiene dalla relazione precedente ponendo p=0 m. e quindi in tale punto l'energia potenziale è
![]()
La diminuzione di energia potenziale implica un equivalente aumento di energia cinetica K. Dato che la particella era ferma, si ha
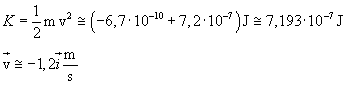
La rotazione di un anello implica movimento di carica, cioè presenza di corrente elettrica. L'intensità della corrente è
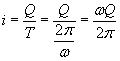
Ruotando entrambi gli anelli si hanno due correnti opposte ad ognuna delle quali è associato un momento di dipolo magnetico perpendicolare al piano della spira e proporzionale all'area della spira
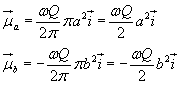
La somma dei due momenti risulta