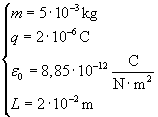
Tre particelle puntiformi, aventi cariche q uguali (q = 2 x 10-6 C) e masse m uguali (m = 5 x 10-3 kg), sono inizialmente fissate ai vertici di un triangolo equilatero di lato L = 2 cm. In un certo istante una delle tre particelle viene liberata e inizia a muoversi per azione delle forze esercitate dalle altre due.
Calcolare, per tale particella:
il modulo della sua velocità v, quando essa si trova a distanza molto grande (infinita) dalle altre due;
la sua posizione, quando il modulo di v è la metà di quello trovato al punto 1.
Un filo di rame (resistività ρ = 1.72 x 10-8 Ω m)
di diametro d = 2 mm forma una spira rettangolare di dimensioni
l × h (l = 0.1 m, h = 6 cm) in un piano perpendicolare a un campo
di induzione magnetica B. Sapendo che il modulo di B varia secondo
la legge B(t)=B0cos ω t, (B0 = 2 T) determinare:
l'energia dissipata per effetto Joule dalla spira nei primi 3/4 di periodo.
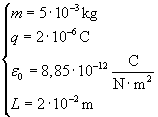
Inizialmente la particella liberata ha energia cinetica nulla ed energia potenziale
Quando la particella si trova a distanza infinita la sua energia potenziale si annulla e la particella ha solo energia cinetica. Per il principio di conservazione dell'energia meccanica
da cui
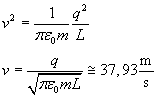
La carica mobile si sposta sull'asse del segmento delimitato dalle altre due cariche. Scegliendo come origine il punto medio di tale segmento e come asse delle ascisse l'asse del segmento, la distanza della carica mobile da ognuna delle altre due è
Quando la velocità è la metà di quella finale l'energia cinetica è un quarto di quella finale: dunque l'energia potenziale è tre quarti di quella iniziale:
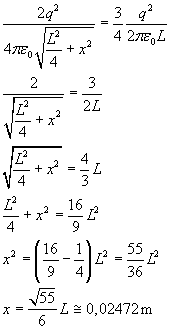
La lunghezza della spira è
e
la sua area è
La sua resistenza è
La f.e.m. istantanea è
e la corrente istantanea
L'energia dissipata nel tempo indicato si ricava integrando la potenza da 0 a
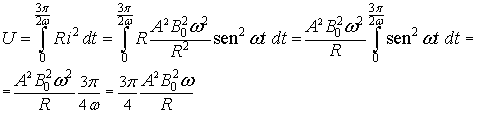
Assumendo ω=60 s-1 risulta
