Due condensatori piani di capacità
e
sono connessi in serie. Ad essi è collegato, in parallelo, un generatore che mantiene
una differenza di potenziale costante
.
Una lastra di dielettrico, con costante dielettrica relativa k=4, viene inserita tra
le armature di C1 così da riempirlo completamente.
Calcolare:
la variazione della carica di C2;
la variazione della d.d.p. ai capi di C1;
la variazione di energia elettrostatica del sistema.
Un filo rettilineo infinito, percorso da una corrente
,
dove I0=10 A e τ=5 s, si trova in un piano in cui giace anche
una spira rettangolare di lati a=6cm e b=12cm, con il lato più lungo
(più vicino e parallelo al filo) alla distanza r=4cm dal filo stesso. Sapendo che
la spira ha una resistenza R=2Ω, calcolare:
la f.e.m. indotta nella spira;
la carica q che percorre la spira nell'intervallo di tempo da zero a ∞.
La capacità totale del sistema è data inizialmente da
La capacità totale del sistema è data alla fine da
La variazione di capacità è quindi
La carica, in modulo, è uguale su tutte le armature dei condensatori in serie, quindi la variazione di carica sulle armature di C2 è
La carica inizialmente presente sulle armature di C1 e C2 è
quindi
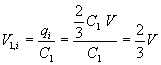
La carica finale sulle armature è
quindi
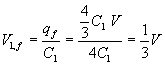
La variazione di potenziale ai capi di C1 è quindi
L'energia immagazzinata nel sistema è esprimibile come
.
A parità di potenziale V si ha quindi
Assumendo un sistema di riferimento cartesiano con asse delle ordinate coincidente con la direzione della corrente nel filo rettilineo, origine sul filo e asse delle ascisse perpendicolare allo stesso, il flusso di induzione magnetica attraverso ad una porzione rettangolare dell'area della spira di altezza b e base dx risulta
Il flusso totale concatenato con la spira è quindi
La f.e.m. indotta risulta
Il valore assoluto della corrente nella spira risulta
Il valore assoluto della carica che percorre la spira si ha integrando la corrente in funzione del tempo
