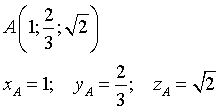
Un punto reale tridimensionale (nel seguito semplicemente punto) è una terna ordinata di numeri reali.
L'insieme di tutti i punti è detto spazio tridimensionale (in seguito semplicemente spazio).
Un punto è normalmente rappresentato da una lettera latina maiuscola.
Ogni numero della terna è una coordinata del punto. Le coordinate, nell'ordine, sono denominate ascissa, ordinata, quota e usualmente rappresentate dalle lettere latine minuscole x, y, z seguite dal nome del punto come deponente.
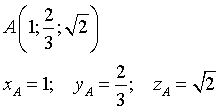
Il punto O(0;0;0) è detto origine.
Ad ogni punto A corrisponde biunivocamente un vettore reale tridimensionale a (nel seguito semplicemente vettore) la cui intensità (o modulo) è la radice quadrata della somma dei quadrati delle ordinate del punto.
I vettori sono usualmente rappresentati dalla versione latina minuscola del punto corrispondente sormontata da una freccetta o stampata in grassetto. Le coordinate del punto sono dette componenti del vettore corrispondente L'intensità è rappresentata dal simbolo del vettore tra barrette verticali.
Un vettore di modulo unitario è detto versore.
Le componenti di un versore u sono i suoi coseni direttori: si pone
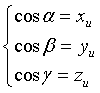
e quindi
Si indicano con i, j, k i versori
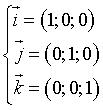
L'utilità dell'abbinamento biunivoco tra punti e vettori consiste nel fatto che mentre gli insiemi di punti sono oggetti suscettibili solo di relazioni insiemistiche (appartenenza, unione, intersezione, parallelismo, perpendicolarità...) gli insiemi di vettori sono strutturati da operazioni, cioè su di essi è definita un'algebra.
Il prodotto m di un vettore v per un numero reale α (che in questo contesto è detto scalare) è il vettore le cui componenti sono i prodotti dello scalare per le componenti di v.
m è un multiplo di v.
La somma di due vettori a e b è il vettore le cui componenti sono le somme delle componenti omologhe degli addendi.
Ogni vettore v può essere rappresentato dalla somma dei prodotti di ognuna delle sue componenti per il versore assiale corrispondente:
Il prodotto scalare di due vettori a e b è la somma dei prodotti delle loro coordinate omologhe. Questa operazione è graficamente rappresentata da un punto (in Inglese dot product).
Il prodotto vettoriale, rappresentato da un segno cruciforme (in Inglese cross product), tra due versori assiali è tale che:
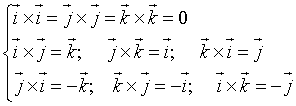
Il prodotto vettoriale è anticommutativo.
Il prodotto vettoriale è distributivo.
Dati i vettori
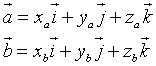
il loro prodotto vettoriale risulta
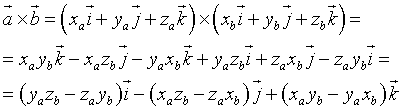
Il prodotto vettoriale può essere più sinteticamente espresso dal determinante
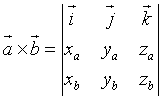
Il prodotto vettoriale è perpendicolare ad entrambi i fattori.
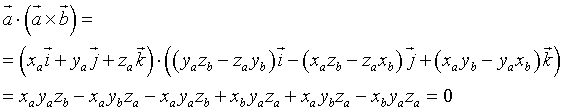
La distanza tra due punti è data dal modulo della differenza tra i vettori corrispondenti.
La seguente applicazione JS, accessibile solo se il browser in uso permette il tag iframe, calcola la distanza tra due punti A e B.
Se il browser in uso non permette il tag iframe, potete aprire la pagina sorgente.
Due vettori individuano un angolo convesso.
Detto θ l'angolo convesso individuato dai vettori a e b, si dice coseno di θ il rapporto tra il loro prodotto scalare e il prodotto dei loro moduli:
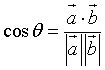
Se il coseno è nullo, i vettori sono mutuamente perpendicolari e viceversa;
se il coseno è positivo, i vettori formano un angolo acuto (< 90°) e viceversa;
se il coseno è negativo, i vettori formano un angolo ottuso (> 90°) e viceversa;
se il coseno è = 1, i loro versori sono coincidenti e l'angolo è nullo e viceversa;
se il coseno è = -1, i loro versori sono opposti e l'angolo è piatto e viceversa;
Come nella geometria piana, dato il coseno, la misura dell'angolo è data dalla funzione arcocoseno o coseno inverso.
Si dice seno di θ il rapporto tra il modulo del loro prodotto vettoriale e il prodotto dei loro moduli:
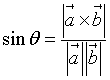
Come nella geometria piana, dato il seno, la misura dell'angolo è data dalla funzione arcoseno o seno inverso.
Esempi
a=i+2j-k e b=-i+j-2k:
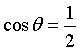: angolo acuto
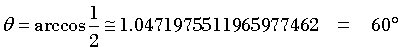
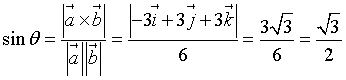
Dato che i seni di angoli supplementari sono uguali, il calcolo dell'angolo convesso θ con l'arcoseno è ambiguo:
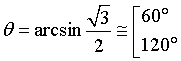
La seguente applicazione JS, accessibile solo se il browser in uso permette il tag iframe, calcola l'angolo tra due vettori a e b.
Se il browser in uso non permette il tag iframe, potete aprire la pagina sorgente.