Rette reali tridimensionali

Rette radiali.

L'insieme dei punti P corrispondenti ai vettori multipli di un versore u = cosα i+cosβ j+cosγ k, cioè i vettori che si ottengono moltiplicando le componenti di u per uno stesso scalare reale τ, è detto retta radiale r_u. u è il suo versore.

I coseni direttori della retta radiale r_u sono coseni direttori di u

Si ha

cioè per ogni punto P di r_u

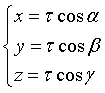
Queste sono le equazioni parametriche della retta radiale r_u in funzione del parametro τ.

Queste equazioni implicano

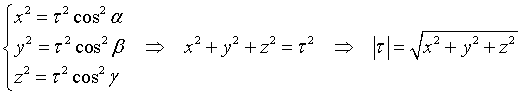
In particolare, dato il punto P(x_P;y_P;z_P) della retta r_u, i coseni direttori della retta r_u, cioè le componenti del suo versore u, sono

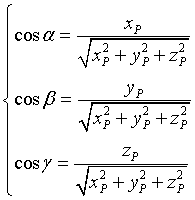
Quindi le equazioni parametriche della retta r_u, cioè della retta per P passante per l'origine O, sono

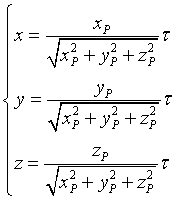
Tutti i punti con coordinate proporzionali a quelle di P corrispondono allo stesso versore e individuano la stessa retta radiale. Quindi ponendo

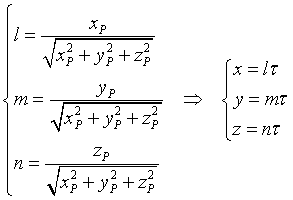
si ottengono equazioni parametriche della retta radiale r_u. I parametri l, m, n sono detti parametri direttori della retta r_u.

Esempi.

Dato A(1;2;2), la retta OA ha equazioni equazioni parametriche

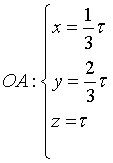
Dato B(2;4;4), la retta OB ha versore uguale a quello della retta OA e quindi coincide con essa.

Retta per due punti.

Dati i punti non coincidenti A(x_A;y_A;z_A) e B(x_B;y_B;z_B) e i corrispondenti vettori a = x_Ai+y_Aj+z_Ak e b = x_Bi+y_Bj+z_Bk, le equazioni parametriche della retta AB si ottengono sommando le coordinate di A alle equazioni parametriche della retta del versore della differenza d = b-a.

I coseni direttori di d sono

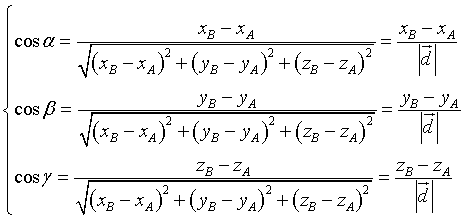
Le equazioni parametriche della retta di questo versore sono

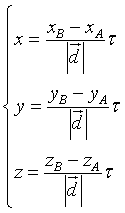
e le equazioni parametriche della retta AB sono

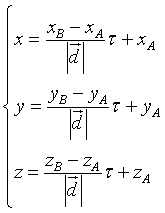
Posto 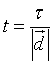, le equazioni parametriche della retta AB possono essere ugualmente espresse da

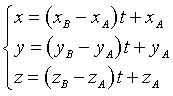
Esempio.

Le equazioni parametriche della retta per A(1;2;-1) e B(2;3;4) sono

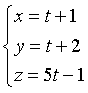
Le coordinate di A si ottengono per t = 0 e le coordinate di B si ottengono per t = 1.

Se la retta AB non è parallela ad alcuno degli assi ordinati, si ha anche

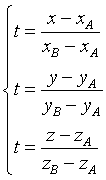
e quindi

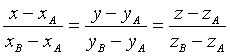
Queste sono le equazioni della retta AB in forma cartesiana.

Esempio: dati i punti A(1;2;-1) e B(2;3;4), si ha:

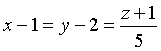
ovvero

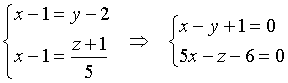
Assumendo come parametro , si riottengono le equazioni parametriche:

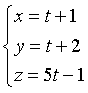
La seguente applicazione JS, accessibile solo se il browser in uso permette il tag iframe, calcola le equazioni parametriche di una retta per due punti.

Se il browser in uso non permette il tag iframe, potete aprire la pagina sorgente.

Rette parallele, incidenti, sghembe.

Rette parallele

Due rette non coincidenti sono parallele se e solo se hanno uguali coseni direttori.

Esempio.

Dati i punti A(1;2;-1) e B(2;3;4) e il punto P(1;1;1), la retta per P parallela ad AB ha coseni direttori uguali a quelli di AB:

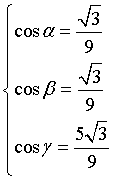
La parallela per P ha equazioni parametriche

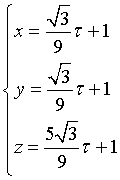
o, più semplicemente,

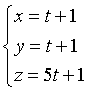
Date le equazioni parametriche di una retta

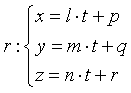
i suoi coseni direttori si possono ricavare:
- Calcolando la parallela per l'origine:
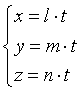
- Calcolando le coordinate del punto della parallela distante 1 dall'origine:
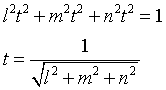
- quindi
  
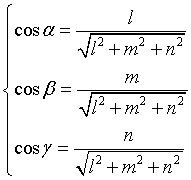
  Esempio.
  
  Data la retta di equazioni parametriche
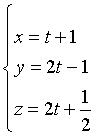
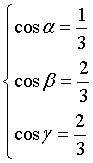
Rette incidenti o sghembe.

Due rette sono incidenti se ammettono un punto comune.

Ovviamente, se sono parallele, non sono incidenti. Se non sono parallele possono comunque non essere incidenti perché appartengono a piani diversi. In questo caso si dicono sghembe.

Esempio: le rette

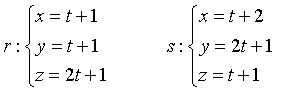
non sono parallele, perché hanno versori diversi, ma non sono nemmeno incidenti perché non esiste alcun punto tale che la sua ascissa soddisfi contemporaneamente le prime equazioni delle due terne.

Angolo tra due rette incidenti.

L'angolo θ tra due rette incidenti r e s è l'angolo dei loro versori. Il coseno di θ coincide con il prodotto scalare di questi versori.

Detti l_r, m_r, n_r i coseni direttori di r e l_s, m_s, n_s i coseni direttori di s, si ha

Se cos θ = 0, le due rette incidenti sono perpendicolari.

Esempio: date le rette

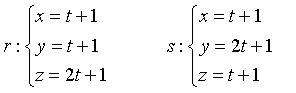
incidenti nel punto I(1;1;1), si ha

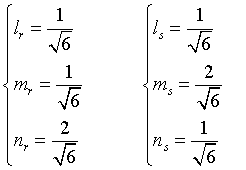
quindi

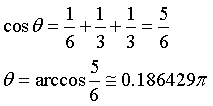
Esempio.

Dati i punti A(1;1;1), B(2;2;3), C(2;3;2), le equazioni in forma cartesiana r e s rispettivamente delle rette AB e AC sono

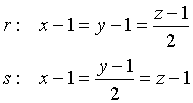
Ponendo in entrambi i casi t=x-1 si ottengono le precedenti equazioni parametriche e l'angolo tra le due rette.

Distanza di un punto da una retta.

Dati la retta r di equazioni parametriche 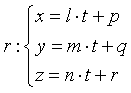e il punto P(x_P;y_P;z_P) esterno a r, la distanza h di P da r si può ottenere nel seguente modo:

si scelgono a piacere due punti distinti A e B di r;
detti a, b e p i vettori corrispondenti a A, B e P, si calcolano le differenze v = b-a e w = p-a;
si calcola l'angolo θ tra v w;
h = |v|·sin θ.

Esempio.

Dati la retta r con equazioni parametriche 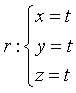e il punto P(1;2;3), scegliendo su r i punti A(0;0;0) e B(1;1;1), risulta:

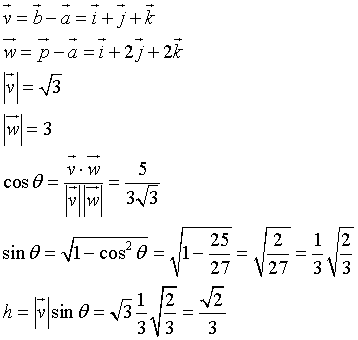
La seguente applicazione JS, accessibile solo se il browser in uso permette il tag iframe, calcola la distanza di un punto da una retta.

Se il browser in uso non permette il tag iframe, potete aprire la pagina sorgente.

Distanza tra due rette.

Date le equazioni parametriche di due rette r e s non coincidenti

se r e s sono parallele, la loro distanza si ottiene scegliendo un qualunque punto P di una e calcolando la distanza di P dall'altra con la procedura descritta nel paragrafo precedente;
se r e s sono sghembe e le loro equazioni parametriche sono

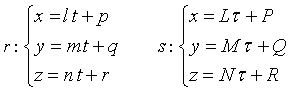
si individuano due punti A∈r e B∈s tali che la differenza d tra i vettori corrispondenti a e b sia perpendicolare a entrambi i versori delle rette r e s. La distanza tra r e s è |d|.

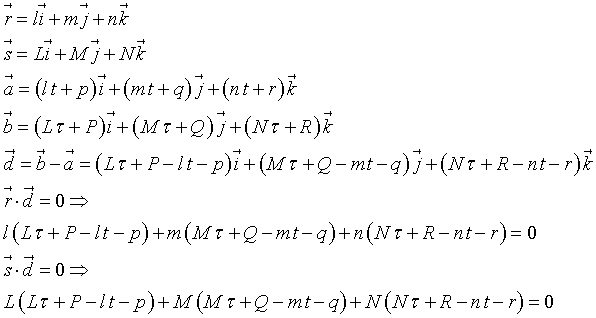
Risolvendo per t e τ il sistema

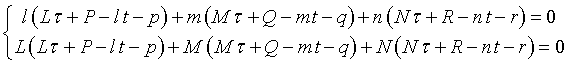
si ottiene il vettore d e quindi il suo modulo che esprime la distanza tra le rette sghembe.

Noti t e τ si ottengono anche i punti A e B delle due rette più vicini tra di loro.

Esempio.

Date le rette r e s con equazioni parametriche

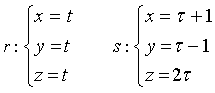
si ottiene il sistema

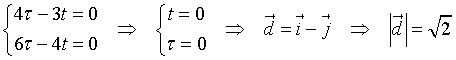
La seguente applicazione JS, accessibile solo se il browser in uso permette il tag iframe, permette di distinguere la relazione tra due rette. Se le rette sono incidenti, calcola il punto di intersezione; se sono parallele o sghembe, calcola la loro distanza.

Se il browser in uso non permette il tag iframe, potete aprire la pagina sorgente.