Dato il versore n
l'insieme dei punti P(x;y;z) individuati dai vettori 
ortogonali a n è il piano Π per l'origine perpendicolare a n.
Due vettori sono ortogonali se e solo se il loro prodotto scalare è nullo, quindi
Questa è l'equazione del piano Π per l'origine perpendicolare a n e, viceversa, n è il versore del piano Π
Tutte le rette perpendicolari a Π hanno versore n e, viceversa, tutte le rette con versore n sono perpendicolari a Π.
Esempio.
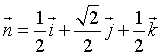
Il piano Π per l'origine perpendicolare al versore n ha equazione
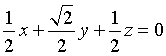
I coefficienti di questa equazione sono definiti a mano di un costante moltiplicativa non nulla, quindi l'equazione di Π può più economicamente essere scritta
Il punto P(1;0;-1) ∈ Π.
In generale, ogni equazione di forma 
è l'equazione di un piano per l'origine
con versore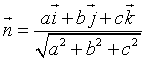 
Esempio.
Il versore del piano di equazione 
è
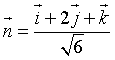
Dati il punto P(xP;yP;zP) e il punto Q(x;y;z) , un'equazione di forma
è l'equazione di un piano perpendicolare al vettore d, differenza tra i vettori corrispondenti a Q e P con versore
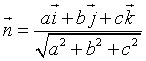
Si ha
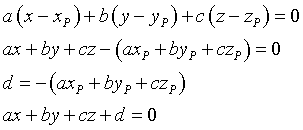
L'ultima delle precedenti equazioni è l'equazione cartesiana di un piano tridimensionale reale di versore n.
Esempi.
Il versore del piano di equazione 
è
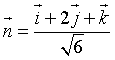
Le intersezioni del piano con gli assi coordinati sono:
Dato il versore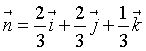 
, il piano per P(1;0;0) di versore n ha equazione
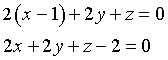
Dati i punti distinti A(xA;yA;zA), B(xB;yB;zB) e C(xC;yC;zC), i coefficienti dell'equazione del piano che li comprende devono soddisfare le seguenti condizioni
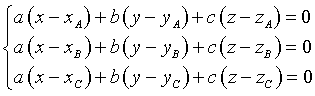
Sottraendo la seconda e la terza di queste equazioni dalla prima, si ha
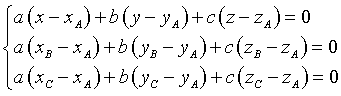
Poiché i parametri a, b e c sono definiti a meno di una costante moltiplicativa non nulla, questo sistema deve essere verificato per qualunque terna ka, kb e kc, quindi deve essere indeterminato rispetto a questi parametri. Ciò implica che
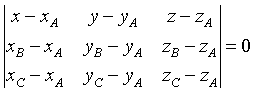
Questa è l'espressione più sintetica dell'equazione del piano per A, B e C. Sviluppando il determinante si ottiene l'equazione lineare.
Esempio.
I punti individuano il piano di equazione
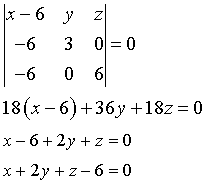
La seguente applicazione JS, accessibile solo se il browser in uso permette il tag iframe, calcola l'equazione del piano per tre punti A, B, C.
Se il browser in uso non permette il tag iframe, potete aprire la pagina sorgente.
Dati la retta r di equazioni parametriche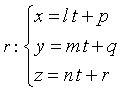 
e il punto C(xC;yC;zC) esterno a r, l'equazione del piano Π per
r e C si può ottenere scegliendo a piacere due punti A e B di r (ad esempio quelli dati dai valori 0 e 1 di t)
e calcolando l'equazione del piano per A, B, C.
Esempio.
Dati il punto C(2;3;4) la retta di equazione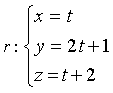 
, due possibili punti A e B sono
A(0;1;2) e B(1;3;3) e dall'applicazione precedente si ottiene Π: 2 x - y + 1 = 0
L'angolo tra due piani coincide con l'angolo formato dai loro versori.
Dati i piani Π1 e Π2 rispettivamente di equazioni
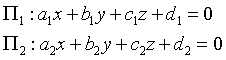
i loro versori sono
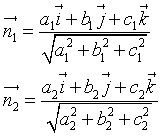
Il coseno dell'angolo θ tra questi versori `
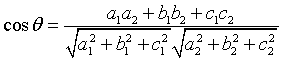
Esempio.
Dati i piani Π1 e Π2 di equazioni
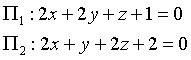
si ha
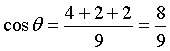
I piani sono perpendicolari se cosθ=0, paralleli (o coincidenti) se cosθ=1.
Se i piani non sono paralleli né coincidenti, la loro intersezione è una retta le cui equazioni si ottengono dal sistema delle equazioni dei due piani.
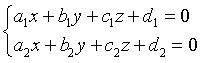
Esempio.
Dati i piani Π1 e Π2 di equazioni
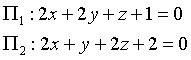
le equazioni della loro intersezione sono
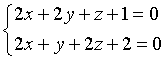
Per ottenere le equazioni parametriche di questa retta si può procedere nel seguente modo:
si sottraggono membro a membro le equazioni, riducendo la variabile x:
si assume y come parametro: y≡t, quindi:
e, dalla prima equazione
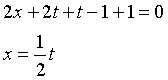
quindi le equazioni parametriche della retta sono
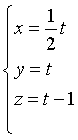
Dati il piano Π di equazione ax+by+cz+d=0 e il punto P(xP;yP;zP), la proiezione di P su Π si può ottenere nel seguente modo:
si calcolano le equazioni parametriche della retta p per P e perpendicolare a Π. Il versore della retta coincide con il versore del piano:
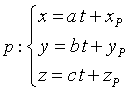
Le coordinate dell'intersezione H di p con Π sono
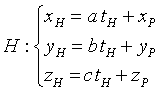
e devono soddisfare l'equazione del piano
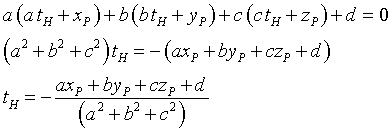
Esempio.
Dati il piano Π di equazione 
e il punto P(2;3;4), si ha H(-8/9;1/9;23/9).
La distanza di un punto P da un piano PΠ è data dalla distanza tra il punto e la sua proiezione H sul piano.
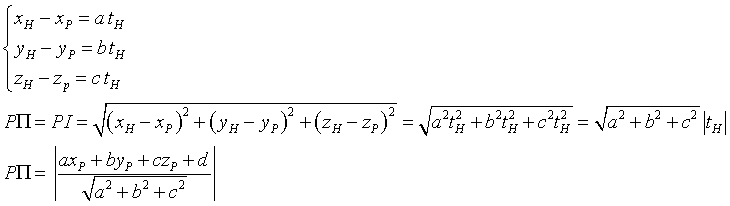
Esempio.
Dati il piano Π di equazione e il punto P(2;3;4), la distanza d=PΠ è
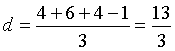
Vedere il quesito 9