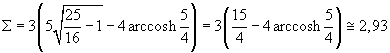
Appunti per i Licei Scientifici
(da Note Didattiche)
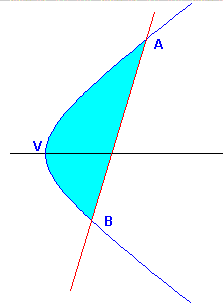
Dati in un piano un'iperbole γ e una retta r che interseca lo stesso ramo di γ in due punti distinti A e B, la parte finita di piano delimitata dall'arco AB di γ e dal segmento AB di r è detta segmento iperbolico.

In particolare, se la retta r è perpendicolare all'asse dell'iperbole γ, il segmento iperbolico si dice retto.
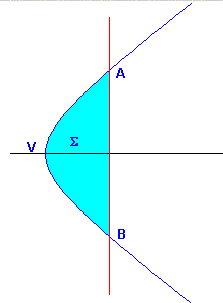
Per calcolare l'area Σ del segmento iperbolico retto individuato nel piano cartesiano xOy dall'iperbole di equazione canonica
![]()
e dalla retta di equazione
![]()
si può procedere nel seguente modo.
Si applica alla configurazione l' affinità che trasforma γ nell'iperbole equilatera di semiasse reale unitario
![]()
La matrice di questa affinità è
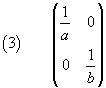
La retta corrispondente alla (2) è quindi
![]()
La configurazione prodotta dall'affinità ha quindi l'aspetto rappresentato dalla figura seguente
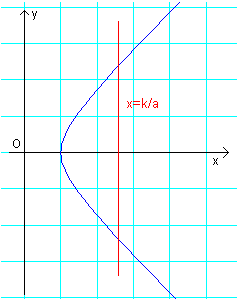
Tracciando i segmenti OA' e OB' si ottiene la seguente figura
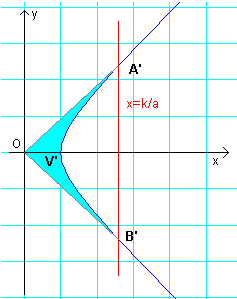
nella quale l'area colorata in azzurro è, per la definizione del coseno iperbolico, l'arcocoseno iperbolico di k/a. L'area Σ' del segmento iperbolico A'V'B' può dunque essere ottenuta dalla differenza tra l'area del triangolo A'OB' e l'arcocoseno iperbolico di k/a.
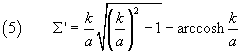
Per una proprietà generale delle affinità l'area Σ' è data dal prodotto dell'area Σ per il determinante dell'affinità:
![]()
da cui
![]()
e infine
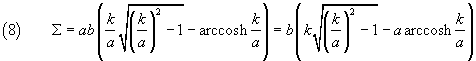
Esempio.
Data un'iperbole di semiassi a=4 e b=3 rappresentata nel suo sistema canonico, l'area del segmento iperbolico retto che si ottiene tagliando il suo ramo di ascisse positive con la retta di equazione x=5 è