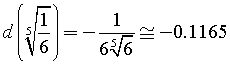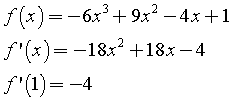
Dato che la funzione è pari, è sufficiente studiarla per x ≥ 0.
La funzione cercata non deve essere derivabile per x = 0. Questo induce a scartare la terza opzione.
La funzione si azzera per x=1, dunque nella seconda opzione k=1. La funzione (per x>0) è
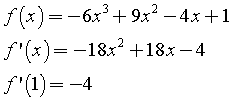
mentre dal grafico si desume che la funzione non è derivabile per x=1.
Per esclusione, va accettata la prima opzione.
L'area della base è data dal doppio dall'integrale
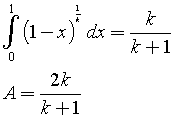
Il volume deve essere al minimo 13 m3
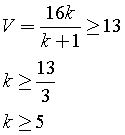
La derivata della funzione per x=0 è
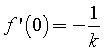
e deve essere ≤ della tangente di -10°.
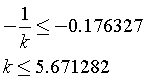
Quindi k=5
![]()
Il volume di combustibile è proporzionale alla metà dell'area di base, che, a serbatoio pieno, risulta
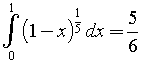
mentre, se non è pieno, dipende dal livello z ed è espressa da
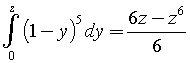
dove la funzione integranda è la funzione inversa di f(x). Il rapporto tra le aree risulta
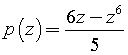
La differenza tr la valutazione dell'amministratore e quella ottenuta è
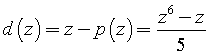
ed è dovuta al fatto ovvio che l'area non è proporzionale all'altezza. Il massimo scarto tra le due valutazioni si ha annullando la derivata di d(z).
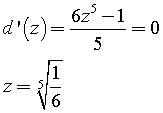
e risulta