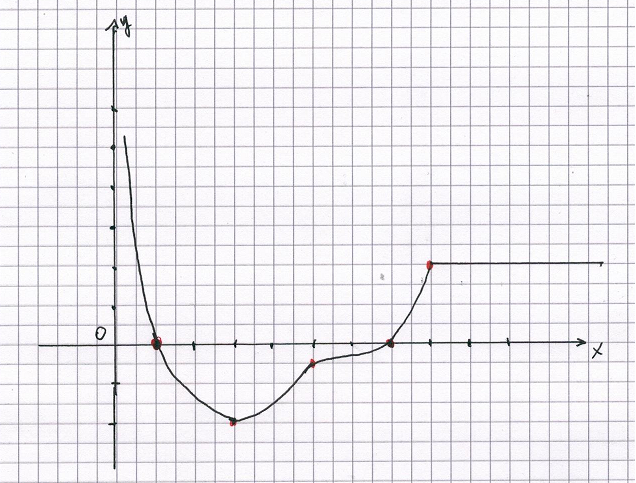
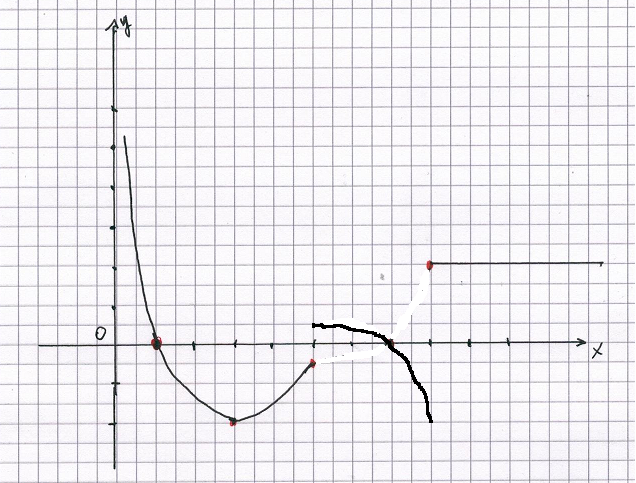
Per x = 0, f(x) non è derivabile; per x→0 da destra, f '(x)→+∞.
Nell'intervallo ]0;1[ f(x) è crescente; f '(x) è positiva e decrescente.
Per x = 1 f '(x) = 0.
Nell'intervallo ]1;3[ f(x) è decrescente; f '(x) è negativa e decrescente.
Per x = 3, f '(x) ha un minimo il cui valore è desumibile dal coefficiente angolare della tangente, cioè -2.
Nell'intervallo ]3;7[ f(x) è decrescente, f '(x) è negativa e crescente. In particolare, f '(5) = -1/2.
Per x = 7, f(x) ha un minimo, f '(x) = 0.
Nell'intervallo ]7;8[ f(x) è crescente; f '(x) è positiva e crescente.
Assumendo che l'arco FG sia un segmento della retta di equazione
![]()
e che f(x) sia derivabile in F, nell'intervallo [8;10], f '(x)=2.
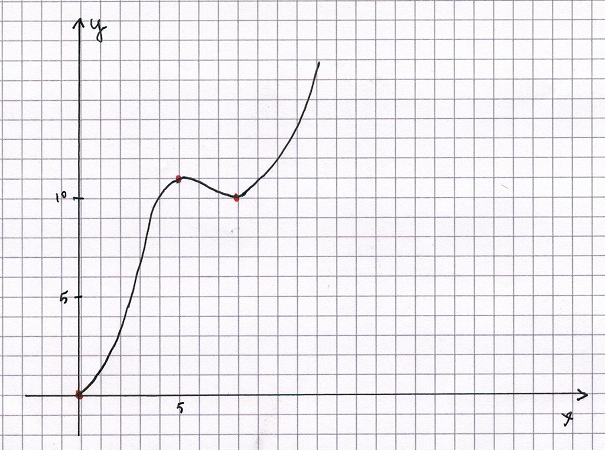
F(0) = 0; nell'intervallo ]0;5[ F(x) cresce fino ad assumere il massimo 11; nell'intervallo ]5;8[ decresce fino al minimo 10; nell'intervallo]8; +∞[ F(x) è crescente.
Inoltre, la funzione f(x) è la derivata prima di F(x), quindi i suoi valori noti rappresentano i coefficienti angolari delle tangenti a F(x); in particolare, per x=0, la tangente ha coefficiente angolare 1; x=1, la tangente ha coefficiente angolare 4; x=3, la tangente ha coefficiente angolare 2; x=5, la tangente ha coefficiente angolare 5; ecc.
f '(x) è la derivata seconda di F(x); dove f '(x) si annulla cambiando di segno (per x=1 e per x=7) F(x) ha flessi.
Il grafico del valore assoluto di una funzione si ottiene dal suo grafico semplicemente sostituendo gli archi di ordinata negativa con i loro simmetrici rispetto all'asse i.
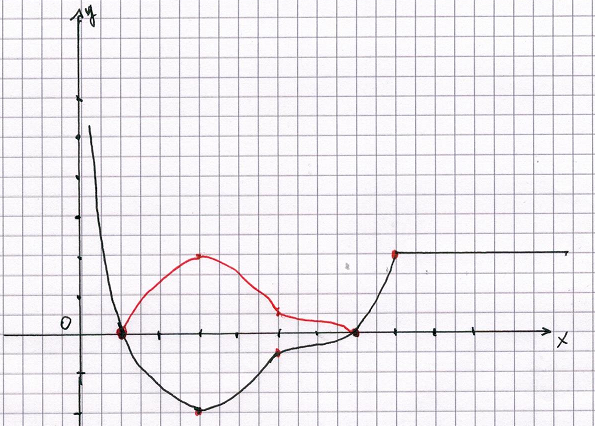
Per ricavare il secondo grafico, si può partire dal grafico del valore assoluto di f(x)
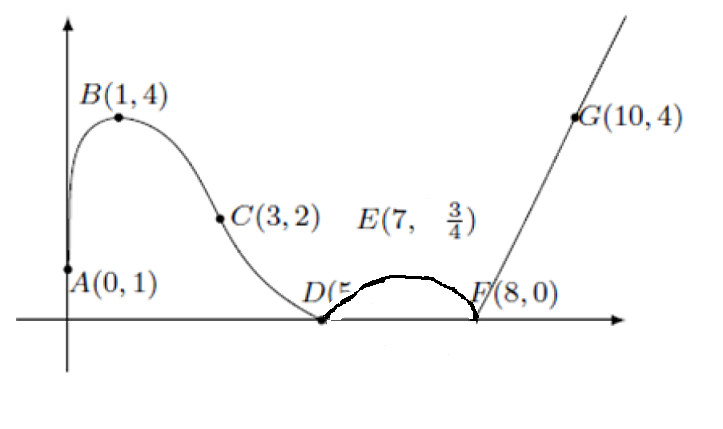
e dedurne l'andamento della derivata con lo stesso metodo usato nel quesito 1.
I cambiamenti sostanziali rispetto all'analisi fatta per il quesito 1 sono dovuti alla non derivabilità del valore assoluto nei punti angolosi D e F, che l'arco DF nel grafico della derivata va sostituito dal suo simmetrico rispetto all'asse x, evidenziando singolarità a salto limitato.
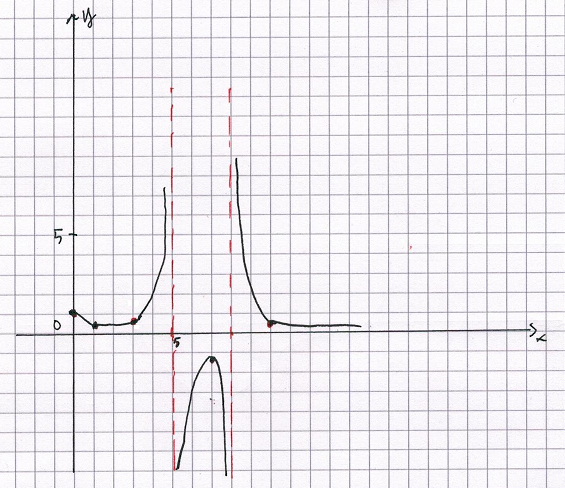
La funzione reciproca di f(x) ovviamente non è definita in cui la f(x) si annulla. La reciproca mantiene il segno di f(x), ma cresce dove la f(x) cala e viceversa e i massimi e minimi locali si invertono: c'è un minimo (1; 1/4) e un massimo (7; -4/3). Tutti gli altri punti noti di f(x) (esclusi gli zeri) mantengono l'ascissa e hanno ordinata reciproca: A(0; 1); C(3; 1/2); G(10; 1/4).
Nell'intervallo [0;8]
Valor medio di f(x)
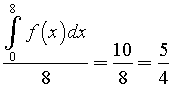
Valor medio di |f(x)|
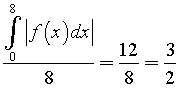
Nell'intervallo [1;7]
Valor medio di f '(x)
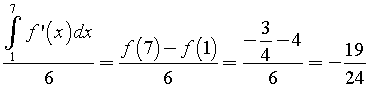
Nell'intervallo [9;10] si ha
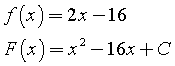
Si sa inoltre che
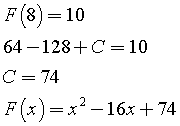
Valor medio di F(x)
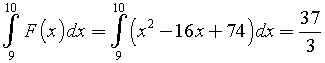
Si è già osservato che nell'origine O la tangente al grafico di F(x) ha coefficiente angolare 1, quindi la sua equazione è y=x
Si è anche osservato che per, x=8, F(x) ha un minimo locale di valore 10. La F(x) è continua e derivabile, quindi in questo minimo la derivata è nulla e l'equazione della tangente è y=10.