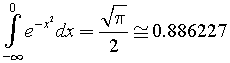
La funzione integranda è pari, dunque
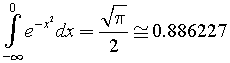
L'integrale da 0 a u è maggiore, dunque u è positivo.
L'integrale A è = 0, poiché la funzione integranda è dispari e gli estremi di integrazione sono simmetrici.
Dal testo si ottiene
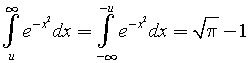
Applicando l'additività degli integrali si ha
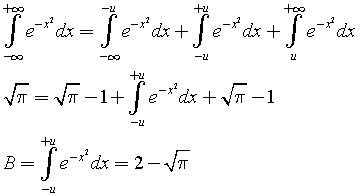
L'integrale C si può calcolare con la sostituzione di variabile
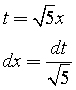
Si ottiene
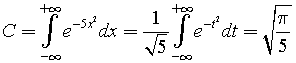
Un rettangolo inscritto ha base 2x e altezza 1-ax2, dunque l'area A(x) e il perimetro P(x) valgono rispettivamente
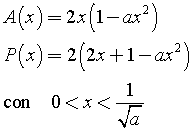
Entrambe le funzioni sono minime agli estremi del dominio, quindi sono inizialmente crescenti, raggiungono un massimo assoluto, poi decrescono. I massimanti si ottengono azzerando le loro derivate.
Per l'area si ha
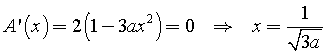
per il perimetro si ha
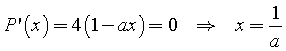
Uguagliando i massimanti si ottiene
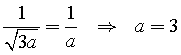
Scegliendo un sistema di riferimento cartesiano con origine nel centro della sfera e asse delle x orientato verso l'alto, l'area di una sezione di spessore infinitesimale risulta
![]()
Il volume è dato da
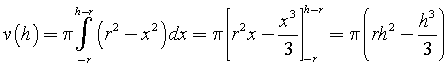
Si può calcolare la probabilità di non sbagliarne alcuna, di sbagliarne solo una o di sbagliarne solo due e poi sommarle. Applicando il teorema di Bernoulli si ha
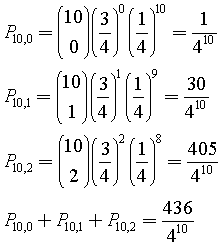
L'equazione parametrica della retta per K perpendicolare al piano risulta
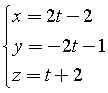
da cui
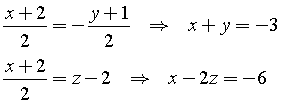
L'intersezione della retta con il piano è data dalla soluzione del sistema
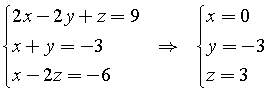
Il raggio della sfera è la distanza tra il centro e il punto di tangenza:
![]()
L'affermazione è vera solo se P(x) è lo sviluppo in serie di MacLaurin di cos(x). Ma se la parola polinomio implica che lo sviluppo è troncato a un numero finito di addendi, allora l'affermazione è falsa.
Per portare la pedina in A (senza andare a zonzo) bisogna fare 7 spostamenti a destra e 7 spostamenti in su, quindi in totale 14 mosse di cui quelle a destra e quelle in su sono tra loro equivalenti. Il numero dei percorsi possibili è uguale a quello delle permutazioni della sequenza AAAAAAABBBBBBB, cioè
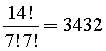
In modo analogo per andare dalla casella di partenza alla casella B, occorrono 3 mosse a destra e 5 in su, cioè
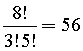
Infine per spostare la pedina da B a A occorrono 4 mosse a destra e 2 in su, cioè
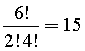
In totale il numero dei percorsi razionali passanti per B è 56*15=840. la probabilità chiesta è il rapporto tra questi e il totale dei percorsi possibili, cioè
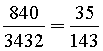
La funzione proposta è la derivata di
![]()
Da F(1)=2e si ottiene
![]()
L'equazione parametrica della seconda retta si può ottenere assumendo x come parametro t:
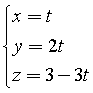
La prima retta r è parallela al vettore ![]()
La seconda retta s è parallela al vettore ![]()
La normale a un piano Π di equazione ax+by+cz+d= è ![]()
r è parallelo a Π se il prodotto scalare vr·n è nullo; s è parallelo a Π se il prodotto scalare vs·n è nullo.
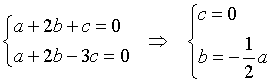
Quindi l'equazione di Π ha la seguente forma
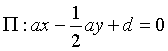
Il punto P(1;0;-2)∈Π, quindi
![]()
In definitiva l'equazione richiesta, a meno di una costante moltiplicativa a, è
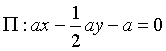
Si ha
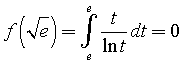
quindi il punto di tangenza T è
![]()
La derivata della funzione integrale è la funzione integranda, dunque
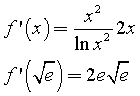
L'equazione della tangente in T risulta quindi
![]()