Ministero dell'Istruzione, dell'Università e della Ricerca
I043 ESAME DI STATO DI ISTRUZIONE SECONDARIA SUPERIORE
Indirizzi: LI02, EA02 - SCIENTIFICO
LI03 - SCIENTIFICO - OPZIONE SCIENZE APPLICATE
LI15 - SCIENTIFICO - SEZIONE AD INDIRIZZO SPORTIVO

(Testo valevole anche per la corrispondente sperimentazione quadriennale)

Tema di MATEMATICA

Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario.

PROBLEMA 1

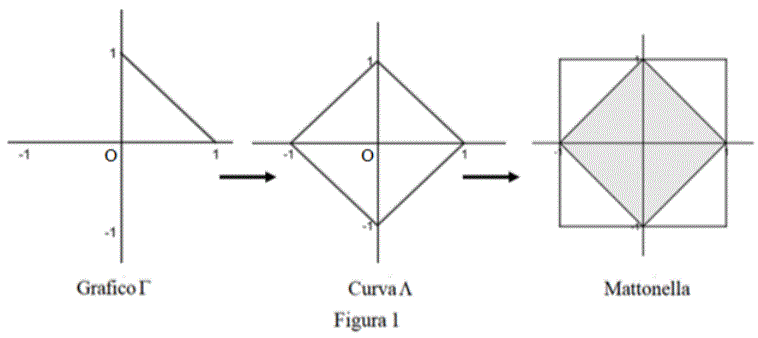
Devi programmare il funzionamento di una macchina che viene adoperata nella produzione industriale di mattonelle per pavimenti. Le mattonelle sono di forma quadrata di lato 1 (in un'opportuna unità di misura) e le fasi di lavoro sono le seguenti:

• si sceglie una funzione y = f(x) definita e continua nell'intervallo [0,1], che soddisfi le condizioni:

  1. f(0) = 1
  2. f(1) = 0
  3. 0 < f (x) < 1 per 0 < x < 1.
• La macchina traccia il grafico Γ della funzione y = f(x) e i grafici simmetrici di Γ rispetto all'asse y, all'asse x e all'origine O, ottenendo in questo modo una curva chiusa Λ, passante per i punti (1,0), (0,1), (-1,0), (0,-1), simmetrica rispetto agli assi cartesiani e all'origine, contenuta nel quadrato Q di vertici (1,1), (-1,1), (-1,-1), (1,-1).
• La macchina costruisce la mattonella colorando di grigio l'interno della curva chiusa Λ e lasciando bianca la parte restante del quadrato Q; vengono quindi mostrate sul display alcune mattonelle affiancate, per dare un'idea dell'aspetto del pavimento.

Il manuale d'uso riporta un esempio del processo realizzativo di una mattonella semplice:

La pavimentazione risultante è riportata di seguito:

1. Con riferimento all'esempio, determina l'espressione della funzione y = f(x) e l'equazione della curva Λ, così da poter effettuare una prova e verificare il funzionamento della macchina.

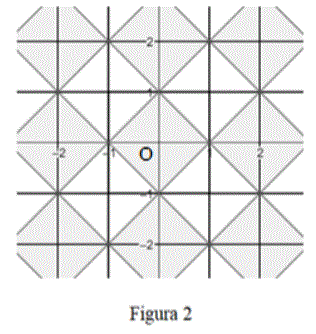
Ti viene richiesto di costruire una mattonella con un disegno più elaborato che, oltre a rispettare le condizioni a), b) e c) descritte in precedenza, abbia f '(0) = 0 e l'area della parte colorata pari al 55% dell'area dell'intera mattonella. A tale scopo, prendi in considerazione funzioni polinomiali di secondo grado e di terzo grado.

2. Dopo aver verificato che non è possibile realizzare quanto richiesto adoperando una funzione polinomiale di secondo grado, determina i coefficienti a,b,c,d ∈ ℜ della funzione f(x) polinomiale di terzo grado che soddisfa le condizioni poste. Rappresenta infine in un piano cartesiano la mattonella risultante

Vengono proposti a un cliente due tipi diversi di disegno, derivanti rispettivamente dalle funzioni , con n intero positivo.

3. Verifica che al variare di n tutte queste funzioni rispettano le condizioni a), b) e c).

   Dette A(n) e B(n) le aree delle parti colorate delle mattonelle ottenute a partire da tali funzioni a_n e b_n calcola ed interpreta i risultati in termini geometrici.

Il cliente decide di ordinare 5.000 mattonelle con il disegno derivato da a₂(x) e 5.000 con quello derivato da b₂(x). La verniciatura viene effettuata da un braccio meccanico che, dopo aver depositato il colore, torna alla posizione iniziale sorvolando la mattonella lungo la diagonale. A causa di un malfunzionamento, durante la produzione delle 10.000 mattonelle si verifica con una probabilità del 20% che il braccio meccanico lasci cadere una goccia di colore in un punto a caso lungo la diagonale, macchiando così la mattonella appena prodotta.

4. Fornisci una stima motivata del numero di mattonelle che, avendo una macchia nella parte non colorata, risulteranno danneggiate al termine del ciclo di produzione.

svolgimento

PROBLEMA 2

Consideriamo la funzione così definita:

con k∈Z

1. Detto Γ_k il grafico della funzione, verifica che per qualsiasi valore del parametro k la retta r_k, tangente a Γ_k nel punto di ascissa 0 e la retta s_k, tangente a Γ_k nel punto di ascissa 1, si incontrano in un punto M di ascissa 2/3.
2. Dopo aver verificato che k = 1 è il massimo intero positivo per cui l'ordinata del punto M è minore di 10, studia l'andamento della funzione f₁(x), determinandone i punti stazionari e di flesso e tracciandone il grafico.
3. Detto T il triangolo delimitato dalle rette r₁, s₁ e dall'asse delle ascisse, determina la probabilità che, preso a caso un punto P(x_P,y_P) all'interno di T, questo si trovi al di sopra di Γ₁ (cioè che si abbia y_P>f₁(x) per tale punto P).

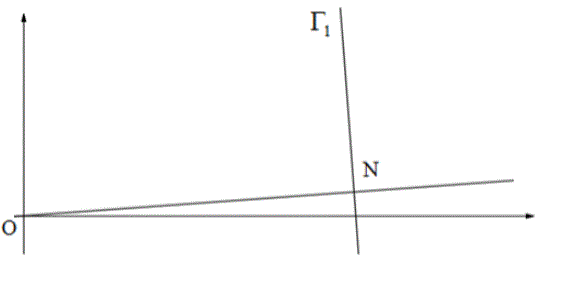
4. Nella figura è evidenziato un punto N∈Γ₁ e un tratto del grafico Γ₁. La retta normale a Γ₁ in N (vale a dire la perpendicolare alla retta tangente a Γ₁ in quel punto) passa per l'origine degli assi O. Il grafico Γ₁ possiede tre punti con questa proprietà. Dimostra, più in generale, che il grafico di un qualsiasi polinomio di grado n>0 non può possedere più di 2n-1 punti nei quali la retta normale al grafico passa per l'origine.

   

svolgimento

QUESTIONARIO

1. Dimostrare che il volume di un cilindro inscritto in un cono è minore della metà del volume del cono.

   svolgimento

2. Si dispone di due dadi uguali non bilanciati a forma di tetraedro regolare con le facce numerate da 1 a 4. Lanciando ciascuno dei due dadi, la probabilità che esca 1 è il doppio della probabilità che esca 2, che a sua volta è il doppio della probabilità che esca 3, che a sua volta è il doppio della probabilità che esca 4. Se si lanciano i due dadi contemporaneamente, qual è la probabilità che escano due numeri uguali tra loro?

   svolgimento

3. Determinare i valori di k tali che la retta di equazione sia tangente alla curva di equazione .

   svolgimento

4. Considerata la funzione 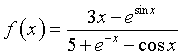, determinare, se esistono, i valori di , giustificando adeguatamente le risposte fornite.

   svolgimento

5. Con una staccionata lunga 2 metri si vuole recintare una superficie avente la forma di un rettangolo sormontato da una semicirconferenza, come in figura:

   

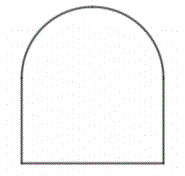
   Determinare le dimensioni dei lati del rettangolo che consentono di recintare la superficie di area massima.

   svolgimento

6. Determinare l'equazione della superficie sferica S, con centro sulla retta r:

   

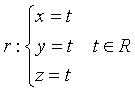
   tangente al piano nel punto T(-4,0,1).

   svolgimento

7. Determinare a in modo che

   

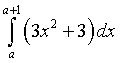
   sia uguale a 10.

   svolgimento

8. In un gioco a due giocatori, ogni partita vinta frutta 1 punto e vince chi per primo raggiunge 10 punti. Due giocatori che in ciascuna partita hanno la stessa probabilità di vincere si sfidano. Qual è la probabilità che uno dei due giocatori vinca in un numero di partite minore o uguale a 12?

   svolgimento

9. Sono dati, nello spazio tridimensionale, i punti A(3,1,0), B(3,-1,2), C(1,1,2). Dopo aver verificato che ABC è un triangolo equilatero e che è contenuto nel piano α di equazione x+y+z-4=0, stabilire quali sono i punti P tali che ABCP sia un tetraedro regolare.

   svolgimento

10. Determinare quali sono i valori del parametro k ∈ ℜ per cui la funzione è soluzione dell'equazione differenziale

    svolgimento

_______________________________________________________________

Durata massima della prova: 6 ore.
È consentito l'uso di calcolatrici scientifiche e/o grafiche purché non siano dotate di capacità di calcolo simbolico (O.M. n. 257 Art. 18 comma 8).
È consentito l'uso del dizionario bilingue (italiano-lingua del paese di provenienza) per i candidati di madrelingua non italiana.
Non è consentito lasciare l'Istituto prima che siano trascorse 3 ore dalla dettatura del tema.