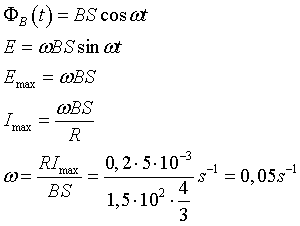La funzione g(x) è continua su tutto ℝ e tende a 0 per x→±∞, quindi il suo codominio è limitato inferiormente e superiormente. La sua derivata prima è
![]()
Dato che il fattore esponenziale è sempre positivo, il segno di g'(x) dipende solo dal segno del fattore polinomio il cui discriminante ridotto è
![]()
Questo discriminante è sempre positivo, quindi il polinomio ha due zeri reali distinti, quindi g(x) ha due estremi relativi che sono anche estremi assoluti.
L'appartenenza del punto A al grafico di entrambe le funzioni f(x) e g(x) implica
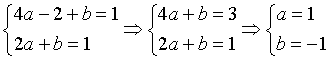
Le funzioni da studiare sono
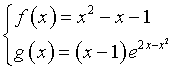
Il grafico di f(x) è una parabola con concavità verso l'alto, vertice in V=(1/2,-5/4), interseca l'asse delle x nei punti di ascisse (1±√5)/2 e l'asse y nel punto di ordinata -1.
Il grafico di g(x) ha asintoto orizzontale sull'asse delle x, ha ordinate positive per x>1, negative per x < 1, interseca l'asse x nel punto di ascissa 1 e l'asse y nel punto di ordinata -1. Inoltre
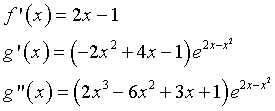
g'(x) ha zeri in (2±√2)/2, cresce nell'intervallo da essi delimitato, con un minimo nel primo e un massimo nel secondo.
g''(x) ha zeri in 1 e (2±√6)/2 che sono le ascisse di tre punti di flesso.
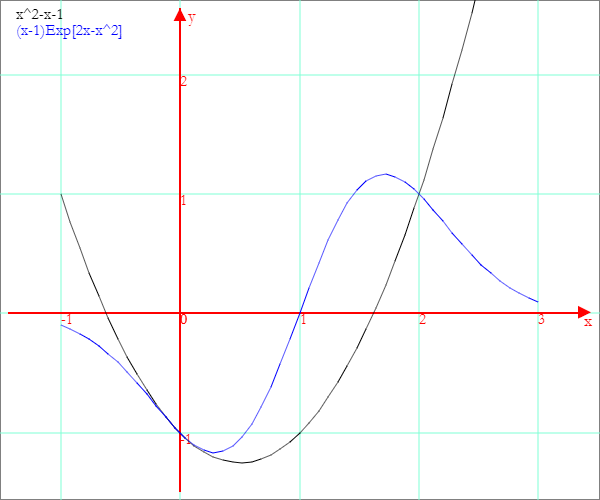
g(1-x)=-g(1+x). Il grafico è simmetrico rispetto al punto (1,0).
f(0)=g(0)=-1. f '(0)=g'(0) = -1. I due grafici sono tangenti nel punto (0,-1).
L'area di S è data dall'integrale
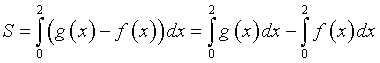
Per la simmetria di g(x) rispetto a (1,0)
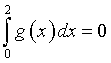
dunque
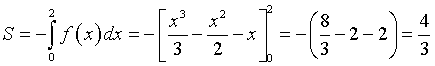
La circuitazione CB del campo magnetico è indipendente dalla forma del percorso e dipende solo dalla somma delle correnti che attraversano la superficie delimitata dallo stesso. Quindi bisogna controllare se le tre correnti indicate attraversano la superficie S.
L'ascissa 1,5 di P1 è minore 1,618, ascissa prossima all'intersezione della parabola con l'asse x. i1 è concatenata con S.
L'ordinata di P2 è minore di g(3/2) ≅ 1,06. i2 è concatenata con S.
L'ordinata di P3 è minore di f(3/2) = -0,25. i3 non è concatenata con S quindi non influisce sul calcolo della circuitazione.
In definitiva
![]()
Se i2 è nulla o equiversa con i1, CB è positiva.
Se i2 è opposta a i1, CB è nulla se i1 e i2 hanno uguale intensità. CB è positiva se l'intensità di i1 è maggiore dell'intensità di i2. CB è negativa se l'intensità di i1 è minore dell'intensità di i2.
Per la legge di Faraday la forze elettromotrice in una spira immersa in un campo magnetico di induzione B variabile nel tempo è
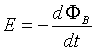
Nel caso proposto