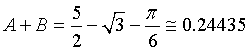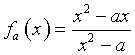sia reale
deve essere 
.Perché la funzione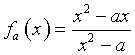 sia reale
deve essere .
Se a<0 la funzione fa(x) è continua e derivabile su tutto ℜ.
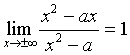
fa(x) ha un asintoto orizzontale di equazione y=1.
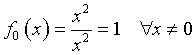. Per x=0 c'è una discontinuità eliminabile.
Se a>0 la funzione fa(x) è discontinua per 
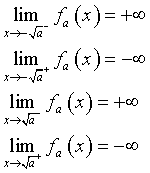
sono asintoti orizzontali.
Anche in questo caso fa(x) ha un asintoto orizzontale di equazione y=1.
Le intersezioni tra fa(x) e il suo asintoto orizzontale si ottengono risolvendo l'equazione
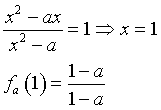
Quindi per ogni a≠1 il grafico di fa(x) passa per il punto P(1;1).
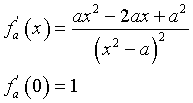
L'equazione della tangente nell'origine è y=x.
Per a≠0, fa(x) è crescente per
Se 0<a<1, 
Se a<0, 
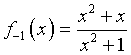
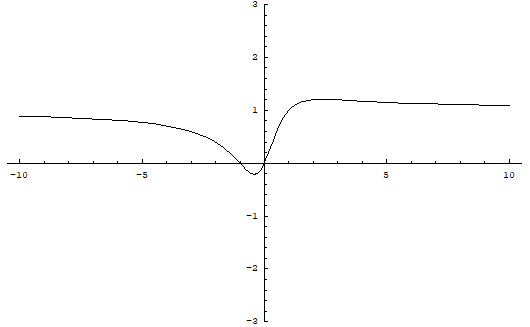
f-1(x) è continua e derivabile su tutto ℜ con asintoto orizzontale y=1.
f-1(x) è crescente per 
;
è decrescente per 
.
Ammette un minimo per 
di ordinata
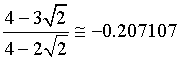e un massimo per
di ordinata
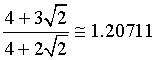
La derivata seconda è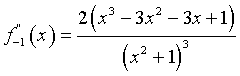 
e si annulla per
in cui si hanno flessi di ordinate
rispettivamente
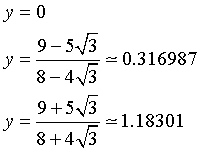
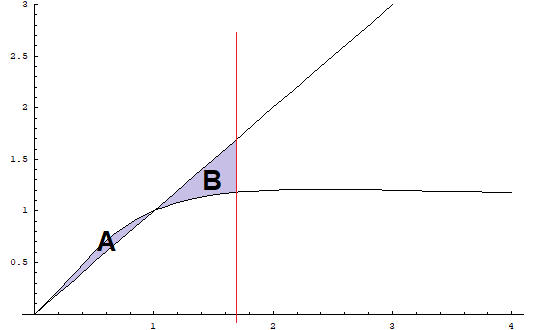
L'equazione della tangente nell'origine è y=x. L'area da calcolare è data dalla somma delle aree A e B evidenziate nella seguente figura.
L'integrale indefinito di f-1(x) è
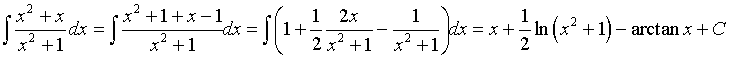
L'area A si ottiene sottraendo dall'integrale di f-1(x) da 0 a 1 l'area di un triangolo di base 1 e altezza 1, cioè 1/2.
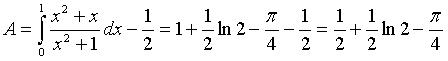
L'area B si ottiene sottraendo dall'area di un trapezio di basi 1 e 
e altezza
, cioè 1,
l'integrale di f-1(x) da 1 a
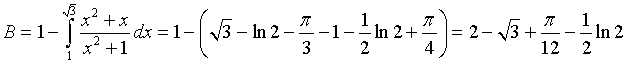
Sommando A e B e semplificando si ottiene
