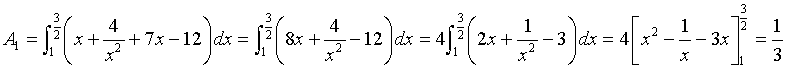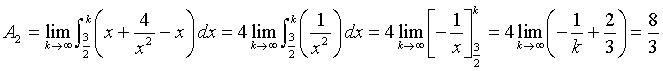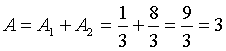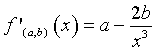e per x=1 vale a-2b.
Questa espressione deve essere uguale al coefficiente angolare della t. Dunque
Il punto P ∈ t, dunque P(1;5). Detto γ il grafico di f(a,b), P ∈ γ dunque a+b=5.
La derivata di f(a,b) è 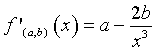e per x=1 vale a-2b.
Questa espressione deve essere uguale al coefficiente angolare della t. Dunque
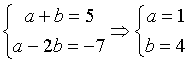
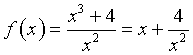
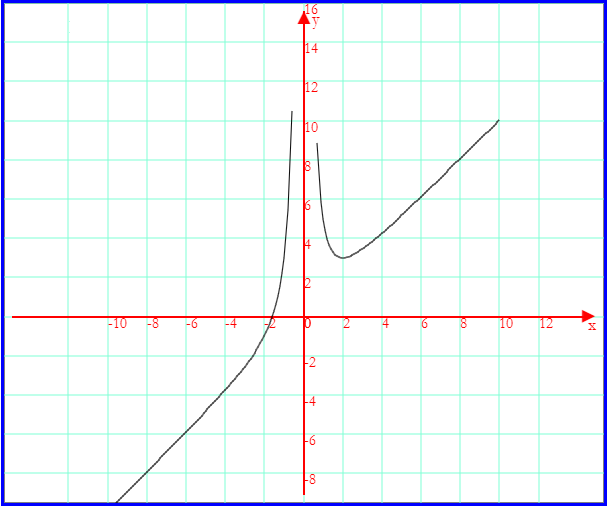
f(x) è reale per x≠0, positiva per x>
e negativa in caso contrario; tende a +∞ per x→+∞ e
x→0; tende a -∞ per x→-∞.
La funzione ha un asintoto verticale nell'asse delle y. La retta di equazione y=x è asintoto obliquo di f(x).
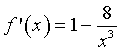
La derivata prima si annulla per x=2 dove la funzione ha un minimo M(2;3), è negativa in 0<x<2 e positiva altrove.
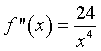
La derivata seconda, nel dominio è ovunque positiva e la funzione ovunque convessa.
Detto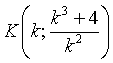 
un punto generico di γ, la tangente a γ
in k ha equazione
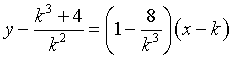
Imponendo il passaggio per P si ottiene
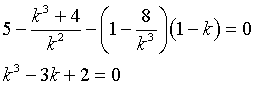
Le evidenti soluzioni di questa equazione sono k=1 e k=-2. Il secondo punto di tangenza richiesto è quindi Q(-2,-1) e l'equazione della tangente per Q è
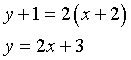
Le intersezioni tra le rette del fascio e γ sono date dalle soluzioni dell'equazione
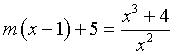
cioè
con ovvia soluzione x=1 dato che P è il centro del fascio e P∈γ. Le altre soluzioni sono quelle dell'equazione
Se m=2 l'equazione è
con due soluzioni coincidenti x=-2, quindi in totale ci sono tre soluzioni.
Se m≠1 e m≠2 l'equazione di secondo grado ha discriminante
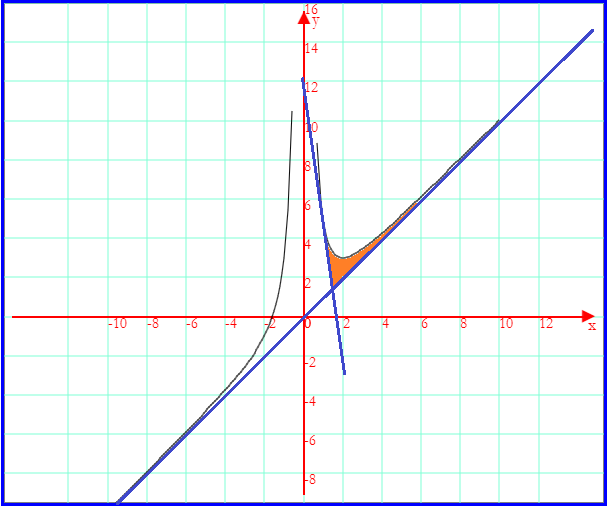
L'area A della regione evidenziata in figura è data dalla somma dell'area A1 della regione comprese tra γ e t per 1<k≤3/2 e l'area A2 della regione compresa tra γ e l'asintoto obliquo per k>3/2.
