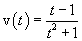
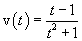
Funzione definita su tutto R.
Il denominatore è sempre positivo. Non ci sono singolarità.
Il segno coincide con quello del numeratore. Quindi la funzione è positiva in ]1 ; ∞[,
negativa in ]-∞ ; 1[, nulla in {1}. Sia A il punto (1 ; 0).
Il grafico interseca l'asse delle ordinate in B(0; -1).
Il grado del numeratore è minore di quello del denominatore. All'infinito la funzione si annulla.
Il grafico ha come asintoto l'asse delle ascisse.
Pendenza
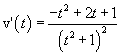
La funzione è derivabile su tutto R. Il segno della derivata coincide con quello del numeratore, quindi
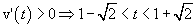
La funzione
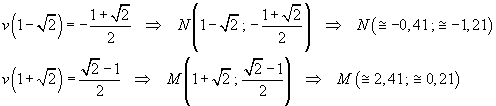
Concavità

La funzione è derivabile due volte su tutto R. Il segno della derivata seconda coincide con quello del numeratore, quindi
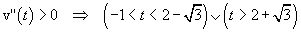
La funzione
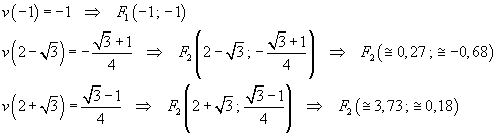
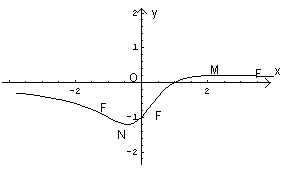
L'equazione oraria risulta

Per il calcolo della velocità media nell'intervallo indicato basta dividere lo spostamento per la durata

L'accelerazione ha estremi relativi dove si annulla la sua derivata, cioè nei punti di flesso, già calcolati, della v(t). Si calcolano quindi i valori di a(t) in tali punti e si individua il massimo tra questi.
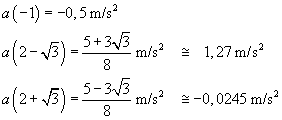
Gli zeri della x(t) si possono rappresentare graficamente come ascisse dei punti di intersezione delle funzioni

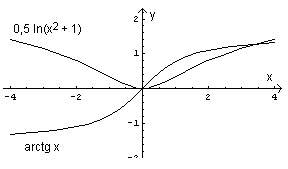
Lo zero cercato è compreso tra 3 e 4. Con il metodo delle tangenti
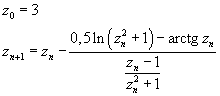
la successione si stabilizza velocemente su 3,50263...
Si propone una implemetazione in Javascript.
function Convergenza(appr)
{
xprec = 0;
x = 3;
while (Math.abs(x-xprec)>appr)
{
xprec = x;
x = xprec-(x*x+1)*(0.5*Math.log(x*x+1)-Math.atan(x))/(x-1);
}
return x;
}
Prova