

Perché la funzione possa rappresentare una densità di probabilità è necessario che
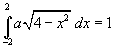
La funzione integranda è pari; conviene quindi
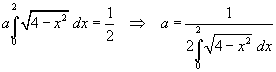
Calcolo dell'integrale
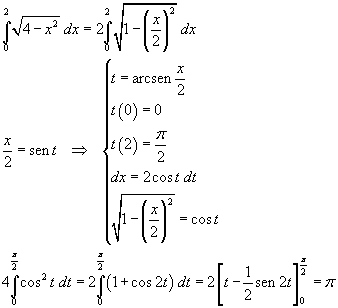
La funzione è quindi

Per -2≤ x ≤ 2 la f(x) ha come grafico una semiellisse di semiassi

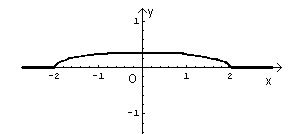
In generale la varianza σ2 si ottiene sottraendo il quadrato della media dalla media dei quadrati. Dato che la f(x) è una funzione pari, la media è zero. La varianza coincide quindi con la media dei quadrati
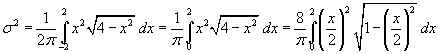
Con la stessa sostituzione usata nell'integrale precedente si ha quindi

In definitiva σ = 1
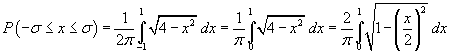
Con la stessa sostituzione usata negli integrali precedenti si ottiene
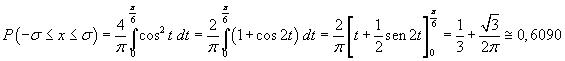
La probabilità che la variabile aleatoria assuma un valore esterno all'intervallo [-σ ; σ] è

La probabilità che la variabile aleatoria assuma un valore esterno all'intervallo [-σ ; σ] cinque volte è

La probabilità che la variabile aleatoria assuma un valore interno all'intervallo [-σ ; σ] almeno una volta su cinque è
