è continua e derivabile su tutto R.La sua derivata
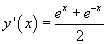è positiva in tutto il dominio,
quindi y(x) è sempre crescente, quindi sempre biunivoca, quindi invertibile in tutto il suo
dominio.La funzione è continua e derivabile su tutto R.
La sua derivata 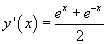è positiva in tutto il dominio,
quindi y(x) è sempre crescente, quindi sempre biunivoca, quindi invertibile in tutto il suo
dominio.
Esplicitando x in funzione di y si ottiene la funzione inversa.
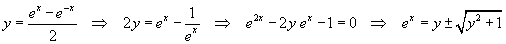
Per la positività dell'esponenziale la soluzione negativa è inammissibile.
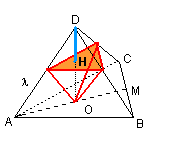
Con riferimento alla figura si ha
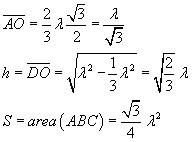
Posto
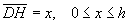
poiché le aree delle sezioni sono proporzionali ai quadrati delle rispettive distanze dai vertici, si ha
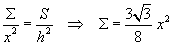
Il volume da massimizzare risulta
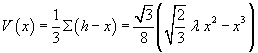
La situazione geometrica rende evidente che, al crescere di x, il volume, inizialmente nullo, in una prima fase aumenta, salvo poi decrescere e annullarsi per x=h. E' sufficiente, in questo caso, cercare lo zero della derivata prima che non coincida con un estremo del dominio per avere il valore massimante.
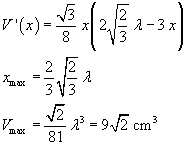
Scrivendo l'unità immaginaria in forma esponenziale si ha
Tutte le radici cubiche hanno modulo 1; le anomalie sono date dai coefficienti degli esponenti
Implementazione Javascript
function Fattoriale(n)
{
if ((n==0)||(n==1))
return 1;
return n*Fattoriale(n-1);
}
function SommaInvFatt(n)
{
somma=0;
for (i=0; i<=n; i++)
somma += 1/Fattoriale(i);
return somma;
}
La somma converge al numero di Nepero e.
La soluzione dell'equazione è data graficamente dall'ascissa del punto di intersezione tra la curva logaritmica e l'iperbole
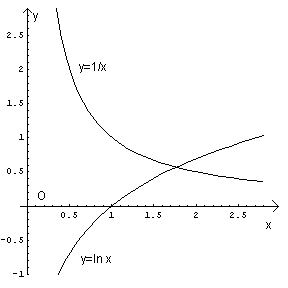
Con il metodo delle tangenti si può costruire una successione che converga allo zero
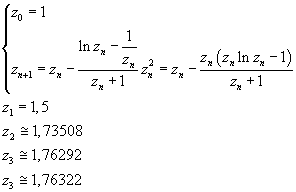
Applicando il teorema di Bayes, la probabilità che un A sia maschio, che un B sia maschio, che un C sia maschio, sono
Le probabilità analoghe per le femmine sono complementari.
La probabilità che il campione scelto sia formato tutto da maschi è
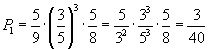
La probabilità che il campione scelto sia formato tutto da femmine è
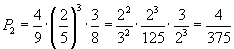
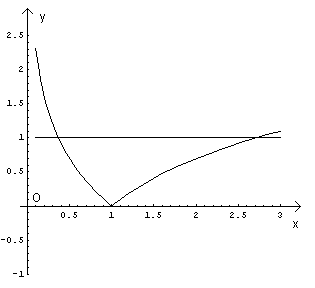
Per x<1 la retta e la curva si intersecano nel punto di ascissa
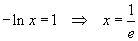
Per x>1 la retta e la curva si intersecano nel punto di ascissa
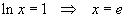
L'area della figura delimitata dalle curve può essere calcolata nel seguente modo
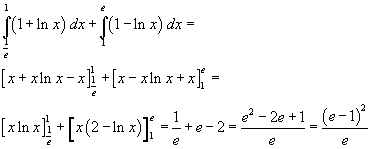
Il lato del quadrato equivalente è quindi
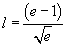
Perché la funzione sia derivabile per x0=1, deve essere continua in tale punto: i limiti da destra e da sinistra devono coincidere. Devono inoltre coincidere i valori della derivata destra e sinistra. Si ottiene
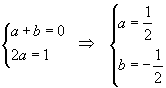
La derivata f'(x) di una funzione f(x) nel punto x0 è data dal limite del rapporto incrementale
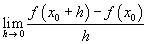
Perché il numeratore sia definito è necessario che x0 appartenga al dominio e sia un punto d'accumulazione del dominio. Inoltre
Calcolando il limite per h->0 si ha
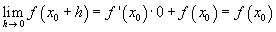
Posto x0+h = x
Il limite coincide con il valore della funzione: dunque sono soddisfatti tutti i requisiti per la continuità.
La lunghezza di un arco di curva di equazione f(x) ed estremi di ascisse a e b è data in generale dall'integrale
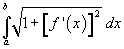
Bisogna quindi valutare l'integrale
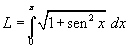
Data la simmetria della curva si può sveltire il calcolo
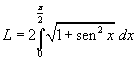
Una valutazione approssimata può essere ottenuta con il metodo dei trapezi: suddividendo
l'intervallo di integrazione in tre sottointervalli di ugual misura π/6 e calcolando
i valori della funzione 
si ha
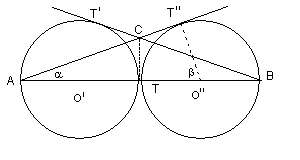
Con riferimento alla figura, nel triangolo rettangolo AO''T'' il seno dell'angolo acuto α è dato dal rapporto tra il cateto O''T'' e l'ipotenusa AO''
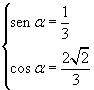
Per l'angolo AO''T'' = β, complementare di α, si ha quindi
L'angolo ACT è congruente a β quindi
