Conviene scrivere la funzione da studiare nel seguente modo:
Dominio di realtà. y(x) è reale
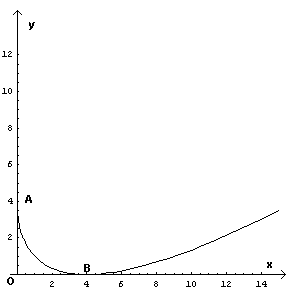
Segno. Nel dominio di realtà la funzione, essendo un quadrato, non è positiva solo se si annulla la base, nel qual caso la funzione si annulla. Dunque la funzione è positiva per ogni x diversa da 4. Il punto B(4;0) è un punto di minimo assoluto.
Tendenze agli estremi.
Il punto A(0;4) è un punto di arresto.
Per x→∞ la funzione diverge positivamente.
Eventuali asintoti obliqui.
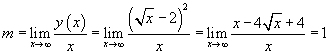
La funzione non ammette asintoti obliqui.
Pendenza.
La funzione cala in ]0;4[, cresce in ]4;∞[ e ha il minimo assoluto, già individuato, in B.
La funzione non ammette derivata per x=0. Nel punto A la tangente alla curva γ è parallela all'asse delle ordinate.
Concavità.
Escluso l'estremo inferiore A, la funzione nel dominio ha sempre concavità positiva.
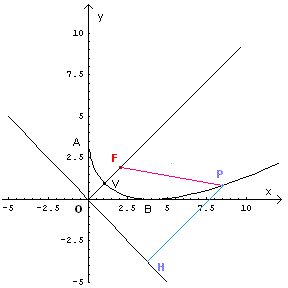
Sia P(x;y) un punto qualunque di γ e H la sua proiezione sulla bisettrice
del secondo e quarto quadrante. Dato che le distanze sono intrinsecamente positive,
conviene verificare in modo del tutto equivalente che
.
Si ottiene
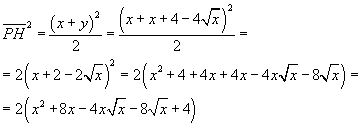
L'uguaglianza è dunque verificata. Ciò significa che la curva γ è un ramo di parabola di fuoco F e direttrice data dalla bisettrice del secondo e quarto quadrante. L'asse di simmetria di questa parabola è la bisettrice del primo e terzo quadrante e il vertice V ha coordinate V(1;1).
Nel sistema ruotato le coordinate del fuoco risultano
e l'equazione
della direttrice
, dunque
l'equazione di γ è
Questa è ovviamente l'equazione di tutta la parabola. Per ottenere solo l'arco con estremo
in A, va imposta la condizione che
Per calcolare l'area del segmento parabolico conviene usare il teorema di Archimede cioè calcolare i 2/3 dell'area del rettangolo circoscritto.
Il segmento AB misura
.
La distanza del vertice V dalla retta AB è
.
L'area del segmento parabolico è dunque
