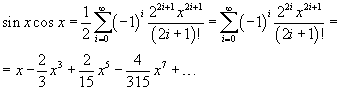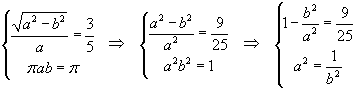
(testo)
Detti a e b i semiassi dell'ellisse, si ha che:
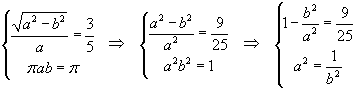
Sostituendo a2 nella prima equazione, si ha
![]()
e quindi
![]()
L'equazione chiesta può essere scritta
![]()
(testo)
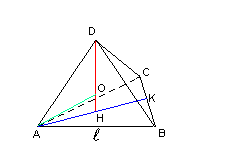
Detto l lo spigolo del tetraedro ABCD di base ABC e altezza DH, si ha
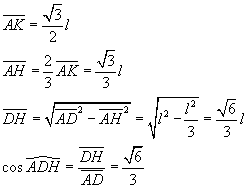
Il punto O su DH, equidistante da A e D, è il centro della sfera circoscritta, quindi r, misura di OA e OD, è il raggio della sfera circoscritta. Nel triangolo isoscele AOD si ha
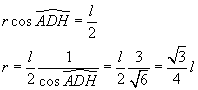
Il volume della sfera circoscritta risulta quindi
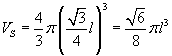
e quello del tetraedro
![]()
Il rapporto tra i due volumi
![]()
(testo)
La negatività della derivata seconda implica che la derivata prima decresce, quindi nell'intervallo I = [x-h ; x] la derivata ha il suo valore massimo nell'estremo inferiore x-h.
Per il teorema di Lagrange, il secondo termine del confronto equivale alla derivata di f(x) in un punto interno all'intervallo I e quindi deve essere minore della derivata in x-h.
Una funzione con le caratteristiche richieste è il logaritmo naturale.
(testo)
Interpretando l'equazione come la risolvente del sistema
![]()
la soluzione grafica dell'equazione è data dall'intersezione delle due curve descritte dalle equazioni
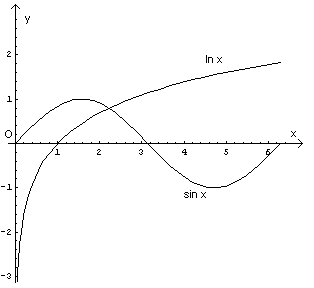
La soluzione è unica e compresa tra 2 e 3. Si può costruire una successione convergente alla soluzione con il metodo delle tangenti. Assunto x0=2, si ha (settare la calcolatrice su rad)
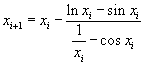
Si ottiene
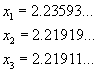
(testo)
La formula è ritenuta bella perché condensa in un'unica relazione alcune delle costanti matematiche più importanti, come 0, 1, π, il numero di Eulero (o di Nepero) e e l'unità immaginaria i.
Dalle note identità di Eulero

si ottiene
![]()
(testo)
Implementazione in Javascript.
function succEuler(n)
{
n = parseInt(n);
if (n<1) return NaN;
somma = 1;
for (i=2; i<=n; i++)
somma += 1/(i*i);
return somma;
}
(testo)
Il metodo di Montecarlo consiste nella generazione di valori casuali di una funzione contando quanti di questi valori appartengono ad un determinato sottinsieme del codominio della funzione stessa. Il rapporto tra il numero di questi valori e il totale dei valori generati fornisce una stima del rapporto tra la misura del sottinsieme e la misura del codominio. La stima è tanto migliore quanto maggiore è il numero di valori generati.
Per approssimare con questo metodo l'area dell'ellisse indicata, conviene limitare il calcolo alla porzione di superficie nel primo quadrante per poi moltiplicarla per 4.
La funzione proposta ha come argomento il numero totale di valori da generare.
function areaEllisse(a,b,n)
{
a = parseFloat(a);
b = parseFloat(b);
n = parseInt(n);
if ((a<=0)||(b<=0))
return NaN;
if (n<100) n=100;
conta = 0;
x = 0;
y = 0;
for (i=0; i<n; i++)
{
x = Math.random();
y = Math.random();
if ((x*x+y*y)<=1)
conta++;
}
return 4*a*b*conta/n;
}
(testo)
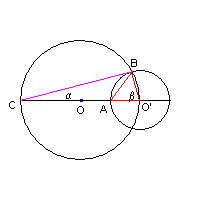
Detto C il punto simmetrico di O' rispetto ad O e tracciato il segmento CB, il triangolo O'CB è rettangolo. Detta α la misura dell'angolo OCB e β la misura dell'angolo CO'B, si ha
![]()
I lati O'A e O'B misurano entrambi r, dunque l'area del triangolo O'AB è
![]()
Il quesito può essere agevolmente risolto anche per via analitica. Scegliendo come origine di un sistema di riferimento cartesiano ortogonale il punto O e come asse delle ascisse la retta OO', le equazioni delle circonferenze risultano

Sottraendo membro a membro si ottiene
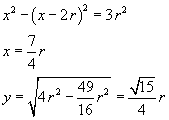
Questa è l'ordinata del punto B, cioè l'altezza del triangolo AO'B la cui area è quindi
![]()
(testo)
Il problema può essere risolto applicando il teorema di Bayes. Se P(R) è la probabilità che uno studente segua Religione e P(i) la probabilità che uno studente sia nella i-esima classe, si ha
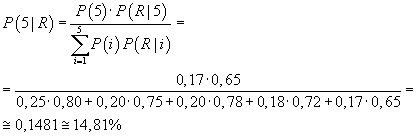
(testo)
Notando che
![]() e che lo sviluppo in serie di MacLaurin del seno è
e che lo sviluppo in serie di MacLaurin del seno è
![]()
si ottiene