Detto P(x;y) un punto del piano, dalla condizione proposta si ha
![]()
Esplicitando y in funzione di x si ha
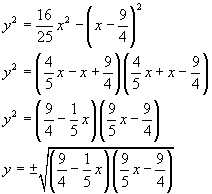
Il luogo dei punti P del piano, per i quali il rapporto e tra la loro distanza da un punto assegnato F e la loro distanza da una retta assegnata d è costante, è una conica di fuoco F, direttrice d e eccentricità e. Se l'eccentricità è compresa tra 0 e 1 (estremi esclusi), la conica è una ellisse. Il luogo proposto Γ è quindi una ellisse.
Nel caso proposto la direttrice coincide con l'asse delle ordinate e l'asse focale dell'ellisse coincide con l'asse delle ascisse.
Le ascisse dei vertici A e B sull'asse focale si ottengono risolvendo l'equazione
![]()
da cui
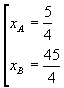
Il semiasse a è la metà della distanza tra i vertici:
![]()
L'ascissa del centro C dell'ellisse è la media delle ascisse dei vertici:
![]()
Il quadrato del semiasse b dell'ellisse può essere ottenuto usando l'equazione esplicita di Γ ponendo x = xC:
![]()
Il grafico di Γ è quindi il seguente
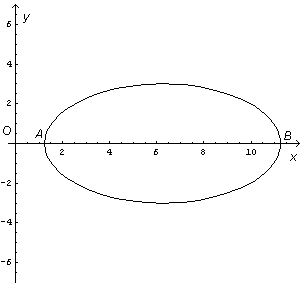
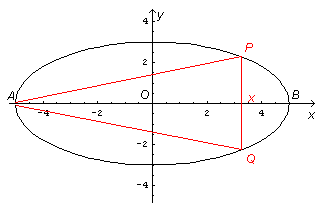
Il problema rimane sostanzialmente immutato se si rappresenta l'ellisse Γ nel suo sistema canonico in cui la sua equazione è data da
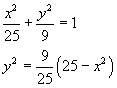
e in cui il vertice di ascissa minore è A(-5 ; 0).
Sia x (-5 ≥ x ≥ 5) l'ascissa dei punti P e Q ottenuti intersecando Γ con una retta perpendicolare all'asse delle ascisse. Il volume del cono che si ottiene ruotando il triangolo APQ attorno all'asse delle ascisse è espresso da
![]()
Si ha quindi
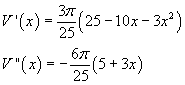
La derivata prima si annulla per x = 5/3, valore per cui la derivata seconda è negativa. Il volume massimo del cono è quindi
![]()
L'area delimitata da Γ è
![]()
Il centro di Γ, data la simmetria, coincide con il suo baricentro e dista xC dall'asse di rotazione. Per il teorema di Guldino il volume del toro risulta
![]()