Dato che la funzione integranda è pari l'equazione proposta è equivalente alla seguente
![]()
e quindi
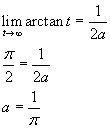
(testo)
Il principio di induzione matematica, nel caso proposto, può essere enunciato nel seguente modo.
Se l'affermazione P(n) è vera per n=1 e, se è vera per n=k, risulta vera anche per n=k+1, allora P(n) è vera per ogni n.
Nel caso proposto si ha
![]() .
.
Quindi
![]()
Inoltre
![]()
Si assume la tesi:
![]()
Allora

Quindi P(n) vale per ogni n.
(testo)
La funzione proposta è reale e positiva per ogni x ∈ R+. La sua derivata prima può essere calcolata con il metodo della derivata logaritmica:
![]()
f'(x) è crescente per
![]() , ha un minimo assoluto per
, ha un minimo assoluto per
![]() ;
;
![]() .
.
Il codominio è quindi 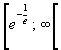
(testo)
Si ha
![]()
La sommatoria è una serie geometrica di ragione q = 0.1. In generale una serie geometrica di ragione q in valore assoluto minore di 1 (e ovviamente non nulla) è tale che
![]()
dunque
![]()
(testo)
Il triangolo isoscele proposto è un triangolo aureo in cui il rapporto tra la base e il lato è
![]()
Il coseno dell'angolo dell'angolo alla base β è
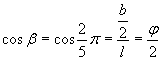
Quindi
![]()
L'altezza del triangolo è
![]()
e l'area
![]()
Il raggio della circonferenza inscritta si può ottenere dal rapporto tra il doppio dell'area e il perimetro
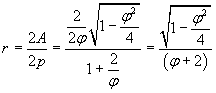
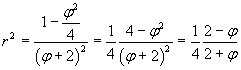
L'area del cerchio inscritto è quindi
![]()
(testo)
Se f(x) è continua per x=0, esiste un intorno I di 0 tale che, ∀ x ∈ I, x>0, f(x) è continua nell'intervallo J = [-x ; x]. Per il Teorema di Weierstrass in tale intervallo f(x) è dotata di massimo e di minimo. Poiché per ipotesi f(x) non è costante, massimante e minimante devono essere diversi e quindi, dato che f(x) è pari, non possono coincidere con gli estremi di J, dunque almeno uno di essi deve essere interno a J. Dato che x può essere piccolo a piacere, uno di essi deve essere uguale a 0.
Il più semplice esempio di funzione f(x) pari, non costante, continua in 0, ma non derivabile in tale punto è
![]()
(testo)
Il rapporto tra i volumi delle sfere è uguale al rapporto tra i cubi dei rispettivi raggi. Il raggio della sfera circoscritta è doppio di quello della sfera inscritta. Il rapporto richiesto è quindi 8.
(testo)
La somma dei coefficienti binomiali è ![]()
La decima potenza di due, in base due, è rappresentata da 10000000000.
Il numero naturale immediatamente minore è il massimo numero che può essere codificato con dieci bit, cioè 1111111111.
(testo)
La velocità istantanea è l'antiderivata rispetto al tempo dell'accelerazione:
![]()
La condizione al contorno permette di risolvere l'indeterminazione
![]()
e quindi
![]()
A sua volta, la posizione istantanea è l'antiderivata della velocità rispetto al tempo:
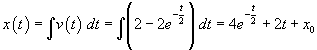
Dalla condizione al contorno si ottiene
![]()
In definitiva, la posizione istantanea è espressa da
![]()
da cui si ottiene
![]()
(testo)
Un metodo numerico diretto per calcolare cosh 1 si basa sullo sviluppo in serie di MacLaurin del coseno iperbolico:
![]()
Per x = 1 si ha
![]()
La somma dei primi 4 termini risulta
![]()
con un errore minore di 1/100. Una calcolatrice scientifica fornisce infatti
cosh 1 ≅ 1.530806...