La funzione f è reale solo se il radicando della radice quadrata non è negativo.
Il dominio di realtà della f è l'insieme dei reali non positivi. In tale dominio la funzione è continua.
Per affrontare la discussione di questo quesito e dei successivi conviene impostare immediatamente lo studio dell'andamento di f nel suo dominio di realtà.
Dato che f è espressa da un valore assoluto essa è sempre non negativa e si annulla per
I due membri dell'equazione sono (nel dominio) entrambi non negativi, dunque
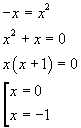
f ha zeri per x = -1 e x = 0.
L'argomento del valore assoluto è positivo per
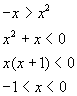
In questo intervallo I1 f è espressa da
mentre per x < -1 (intervallo I2) f è espressa da
In I1 si ha
La derivata non è definita in 0 e diverge per x→0. Nell'origine del sistema di riferimento il grafico della f è tangente all'asse delle ordinate.
Il limite della derivata per x→-1 da destra è
In un intorno sinistro di -1 f è espressa da f2, opposta di f1. Dunque anche la derivata risulta opposta a quella di f1 e così anche il suo limite nello stesso punto di accumulazione -1. Si ha quindi
Derivata sinistra e destra convergono a valori finiti ma diversi. Per x = -1 f non è derivabile e il grafico di f presenta un punto angoloso.
Per produrre il grafico richiesto, conviene, tenendo conto dei risultati acquisiti nei punti precedenti, ottenere il diagramma dell'argomento a(x) del valore assoluto e procedere poi a 'raddrizzare' eventuali rami di tale diagramma con ordinate negative tracciando i loro simmetrici rispetto all'asse delle ascisse.
Limite di a all'estremo inferiore del dominio.
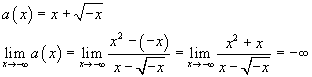
Per x→-∞ la funzione diverge negativamente.
Eventuale asintoto.
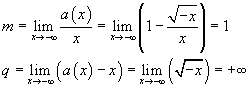
a non ammette retta asintotica.
Pendenza di a.
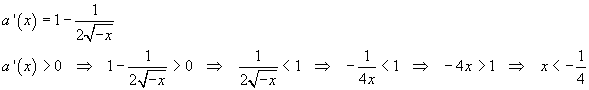
a cresce per
,
cala per
,
ha un massimo relativo per
di valore
.
Concavità di a.
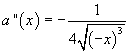
Per x <0 la derivata seconda è negativa. La concavità è costantemente negativa.
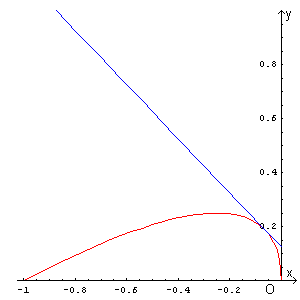
Diagramma di a(x)
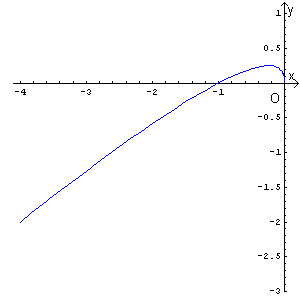
Diagramma di f(x)
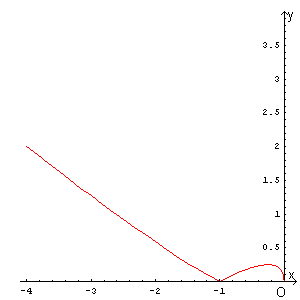
Si ha
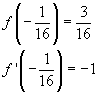
L'equazione della tangente richiesta risulta
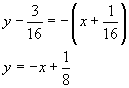
Perché la funzione φ proposta rappresenti una densità di probabilità è necessario che
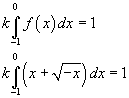
L'integrale vale
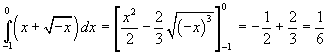
Dunque k deve essere uguale a 6.