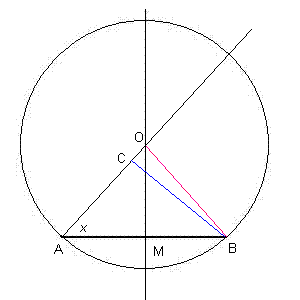
Nella costruzione proposta, la misura x varia nell'intervallo [0; π/2[; per valori negativi si avrebbe una figura simmetrica sostanzialmente equivalente.
Si ha immediatamente
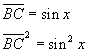
Inoltre
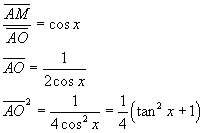
Si ottiene quindi
Prescindendo, come richiesto dal testo, dal dominio geometrico e assumendo quindi la variabile x come
generica variabile reale, date le singolarità della funzione tangente, la funzione f(x) è definita reale
.
In tale dominio f è pari, quindi il suo grafico risulta simmetrico rispetto all'asse delle ordinate e, dato che f non è costante e non ha singolarità per x=0, presenta un estremo relativo per x=0.
f ha la stessa periodicità della funzione tangente: il suo periodo ha quindi ampiezza π.
Data la parità di f, conviene studiarne l'andamento nell'intervallo ]-π/2;+π/2[.
f è una somma di quadrati con una costante positiva, quindi è positiva in tutto il suo dominio.
Il quadrato della tangente diverge positivamente per
; conseguentemente anche f diverge
positivamente per tali valori per i quali quindi il diagramma di f ha asintoti verticali.
La derivata di f risulta
Nell'intervallo [0 ; π/2[ la somma a secondo membro assume sempre valori non negativi e si annulla solo
per x=0. Per simmetria, nell'intervallo ]-π/2 ; 0[ la derivata è sempre negativa. Dunque f
decresce in ]-π/2 ; 0[, cresce in ]0 ; π/2[ e ha un minimo
.
Riscrivendo f'(x) nel seguente modo
e derivando rispetto a x si ha
La derivata seconda, nell'intervallo ]-π/2 ; +π/2[ è sempre positiva. Dunque la concavità è sempre positiva e non ci sono flessi.
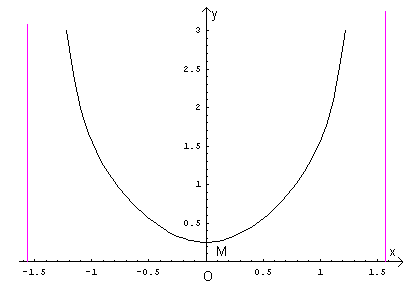
diagramma di f(x) nell'intervallo
Nel dominio geometrico
il minimo di f è l'ordinata
del punto M già determinato cioè 1/4.
Il valore medio di f nell'intervallo
si ottiene calcolando
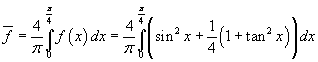
L'antiderivata del primo addendo della funzione integranda è
L'antiderivata del secondo addendo è
Per la regola di Torricelli si ha
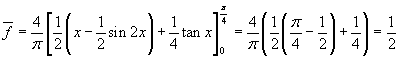
L'equazione proposta è equivalente a
Graficando separatamente i due membri di tale equazione si ottiene
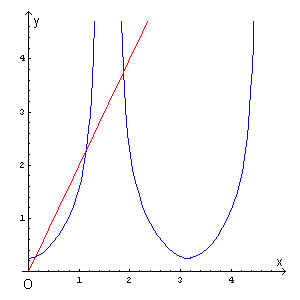
Le due curve, nell'intervallo [0 ; π] si intersecano tre volte. Ciò significa che l'equazione proposta ammette tre zeri.
La funzione
, ottenuta dalla differenza tra una
funzione a concavità nulla e una a concavità positiva, ha sempre concavità negativa. Volendo approssimare il minore
degli zeri positivi si può procedere con l'algoritmo delle tangenti assumendo com valore iniziale x0 = 0.
Si ha
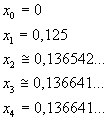
Il minore degli zeri positivi vale circa 0,136641 con approssimazione dell'ordine del milionesimo.