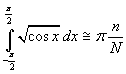, separando le variabili,
si ottiene(testo)
Da , separando le variabili,
si ottiene
Integrando entrambi i membri
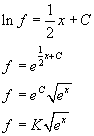
Da f(0)=1 si ha K=1, quindi la funzione richiesta è
(testo)
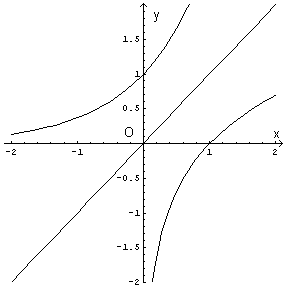
Le due funzioni sono l'una l'inversa dell'altra, dunque i loro grafici sono simmetrici rispetto alla bisettrice β del primo e terzo quadrante. Per determinare i loro punti di distanza minima è sufficiente determinare, ad esempio, il punto dell'esponenziale più vicino a β.
Detto 
un punto dell'esponenziale,
la sua distanza da β risulta
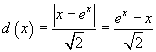
Perché d(x) risulti minima è necessario che si annulli la sua derivata prima:
Per x=0 la derivata seconda è positiva, dunque il punto P(0;1) è quello più vicino a β e conseguentemente a Q(1;0), il suo simmetrico rispetto a β.
(testo)
Il perimetro di t1 misura 3m. I triangoli successivi hanno perimetri in successione geometrica di ragione q = 1/2. Dunque la somma di tutti i perimetri è espressa da
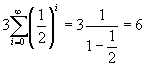
(testo)
L'equazione assegnata è equivalente alla seguente
Graficando separatamente minuendo e sottraendo del primo membro si ha
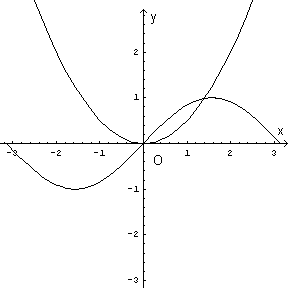
Il grafico evidenzia la presenza di una soluzione compresa tra 1 e 2.
In effetti, considerando la funzione
(continua su tutto R) si
osserva che agli estremi di tale intervallo essa assume valori di segno diverso e quindi, per il teorema di continuità
di Bolzano, deve azzerarsi all'interno di tale intervallo.
Lo zero in questione può approssimarsi con il metodo delle tangenti, assumendo
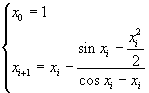
Si ottiene (ovviamente gli argomenti delle funzioni circolari vano espressi in radianti)
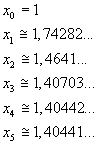
La successione si stabilizza a livello dei decimillesimi, dunque la precisione richiesta è ampiamente conseguita.
(testo)
Il volume generato dalla rotazione dell'arco di sinusoide attorno all'asse delle ascisse risulta
Per uno dei teoremi di Guldino, lo stesso volume può essere ottenuto moltiplicando la superficie delimitata dall'arco di sinusoide e dall'asse delle ascisse per la lunghezza della circonferenza tracciata nella rotazione dal baricentro G. Indicando con yG l'ordinata del baricentro, si ha
Uguagliando i due valori si ottiene
Data la simmetria dell'arco rispetto alla retta di equazione x=π/2, le coordinate di G risultano quindi
(testo)
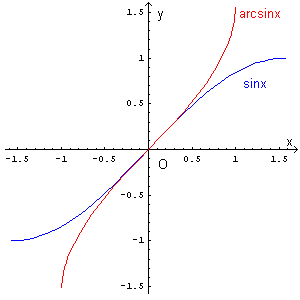
Poiché la funzione arcoseno è la funzione inversa del seno, il suo grafico può essere immediatamente ottenuto da
quello della funzione seno nell'intervallo
tracciandone il simmetrico
rispetto alla bisettrice del primo e terzo quadrante.
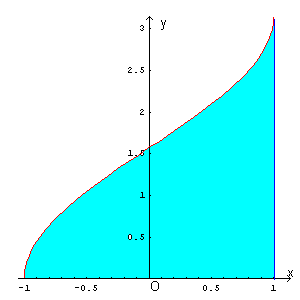
Il grafico della funzione f(x) proposta può essere ottenuto da quello dell'arcoseno con una traslazione di +π/2 lungo l'asse delle ordinate. L'area da calcolare è quindi quella evidenziata in figura.
Se si completa il rettangolo di base 2 e altezza π come nella figura seguente
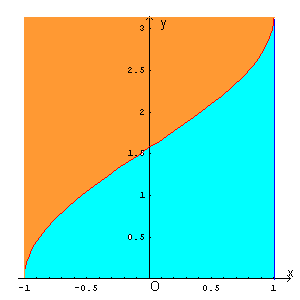
è immediato osservare che l'area richiesta, date l'evidente simmetria, è metà di quella di tale rettangolo e quindi vale π.
(testo)
Il principio di induzione matematica, nel caso proposto, può essere enunciato nel seguente modo.
È data la proposizione
.
Se la proposizione P(n) è vera per n=1 e, se è vera per n=k, risulta vera anche per n=k+1, allora P(n) è vera per ogni n.
Nel caso proposto si ha
. Affermazione evidentemente vera.
Assunta come valida la proposizione
, si ha
In definitiva:
Quindi P(n) vale per ogni n.
(testo)
La probabilità che chi ha votato sia una donna è
, mentre la probabilità che
chi ha votato sia un uomo è
.
La probabilità che una donna voti la lista A è
, mentre la probabilità che
un uomo voti la lista A è
.
Per il Teorema di Bayes la probabilità richiesta risulta:
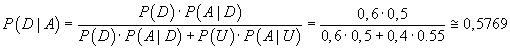
Più intuitivamente si può anche procedere nel seguente modo:
(testo)
La velocità istantanea della particella è data dall'integrale rispetto al tempo della sua accelerazione:
La posizione istantanea della particella è data dall'integrale rispetto al tempo della sua velocità:
Dunque
(testo)
Il Metodo di Montecarlo, formalizzato negli anni '40 del secolo scorso da John von Neumann e Stanislaw Marcin Ulam, consiste essenzialmente nella generazione di un grande numero N di valori casuali di una grandezza, ottenibili tramite la funzione random() di un linguaggio di programmazione, nella conta del numero n di quanti di tali valori possiedono una proprietà prefissata e nel calcolo del rapporto tra n e N.
Per approssimare il valore dell'integrale proposto con un Metodo Montecarlo, si può procedere nel seguente modo.
,
si incrementa di un'unità un contatore che al termine del ciclo avrà valore n.