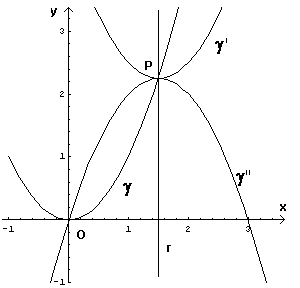
(a cura di Roberto Bigoni)
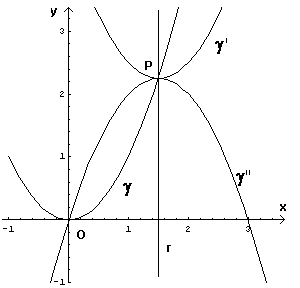
Il vertice di γ' e γ'' Ŕ il punto P ( λ ; λ2 ) e γ' e γ'' hanno direttrici parallele all'asse delle ascisse.
La distanza fuoco-vertice e la distanza vertice-direttrice per le tre parabole Ŕ 1/4.
Per γ' si ha dunque
![]()
La parabola Ŕ il luogo dei punti equidistanti dal fuoco e dalla direttrice, quindi
![]()
Sviluppando i quadrati, semplificando ed esprimendo y in funzione di x si ha
![]()
Per γ'' si ha
![]()
Con procedura analoga a quella adottata per γ' si ottiene
![]()
Come viene eloquentemente indicato dal grafico e come Ŕ ovvio, la γ', che ha asse parallelo a quello di γ, uguale distanza focale e ugual concavitÓ, risulta da una traslazione di γ
![]()
Nel quesito precedente si sarebbe potuto traslare l'equazione di γ per ottenere pi¨ direttamente l'equazione di γ'.
La γ'' pu˛ essere ottenuta direttamente calcolando la simmetrica di γ rispetto al punto
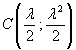
Le equazioni della simmetria centrale risultano
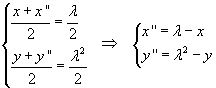
Sulla natura delle trasformazioni s'Ŕ giÓ detto.
Le traslazioni non hanno nÚ punti uniti nÚ rette unite; le simmetrie centrali hanno come punto unito il centro di simmetria.
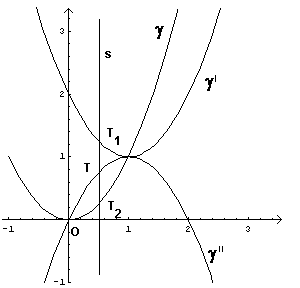
Le parabole, per λ = 1, hanno le seguenti equazioni
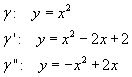
Le coordinate dei punti T, T1, T2 risultano
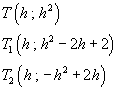
Le distanze contemplate nella funzione z sono
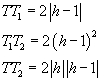
La funzione z ( h ) Ŕ quindi
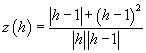
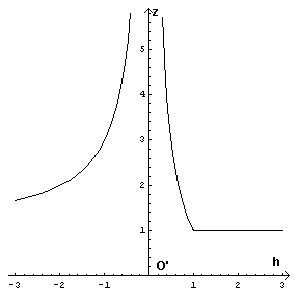
z ( h ) ha singolaritÓ in 0 e 1. La singolaritÓ in 1 Ŕ eliminabile, per cui nel dominio ]-∞ ; 1[ U ]1 ; ∞[ il suo andamento coincide con quello di
![]()
z ( h ) nel dominio Ŕ sempre ≥ 1.
Per h > 1
![]()
la funzione Ŕ costante e il suo grafico Ŕ una semiretta parallela all'asse delle ascisse.
Per 0 > h > 1
![]()
z ( h ) si comporta come una funzione omografica di asintoti h = 0 e z = -1.
Per h < 0
![]()
z ( h ) si comporta come una funzione omografica di asintoti h = 0 e z = +1.
![]()