Problema 3

(a cura di Roberto Bigoni)

  1.  

    fig. 50

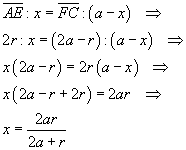
    I triangoli AEF e PQF sono simili: i loro lati sono proporzionali alle loro altezze, quindi

    fig. 51

    I triangoli AEC e RSC sono simili: i loro lati sono proporzionali alle loro altezze, quindi

    fig. 52

    Per l'unicità del quarto proporzionale segue

    fig. 53

  2.  

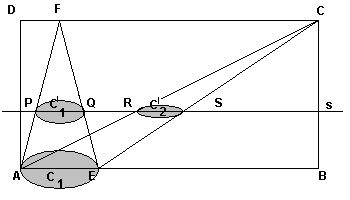
    fig. 54

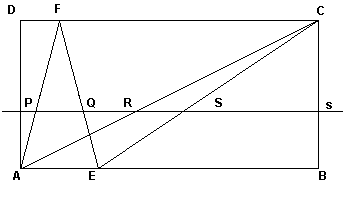
    La superficie laterale del cono T1 è generata dalla rotazione del lato AF attorno all'altezza relativa alla base AE del triangolo AEF. In particolare la sezione C '1 è generata dalla rotazione del punto P ed è quindi una circonferenza.

    La sezione C '2, in quanto sezione conica chiusa, o è una circonferenza o è un'ellisse. I coni T1 e T2, avendo ugual base e ugual altezza, sono equivalenti. Applicando inversamente il principio di Cavalieri, le loro sezioni equidistanti dalle basi sono equivalenti. Se C '2 fosse un'ellisse, avrebbe un semiasse di misura diversa da RS e non sarebbe equivalente a C '1. Quindi C '2 è una circonferenza.

  3. I coni T1 e T2 sono equivalenti. Per entrambi il volume è un terzo del volume del cilindro di ugual base e ugual altezza.

    fig. 55

  4.  

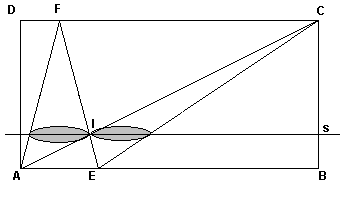
    fig. 57

    C '1 e C '2 risultano tangenti esternamente quando la retta s passa per il punto I di intersezione tra i segmenti AC e EF. Indicando con x la distanza di I da AB e osservando la similitudine dei triangoli AEI e CFI si può scrivere

    fig. 58

Valid XHTML 1.0!