Γ1 è per definizione l'equazione
dell'ellisse di fuochi A e B e
semiasse ![]() .
.
A e B sono sull'asse delle
ascisse e simmetrici rispetto all'origine, quindi il sistema
Oxy è il sistema canonico e l'equazione
dell'ellisse è del tipo
![]() con
con
f = 1.
Dati a e f si ricava
immediatamente b:
![]()
e quindi l'equazione di Γ1 è
![]()
Γ2 è per definizione l'equazione della
circonferenza di centro B e raggio
![]() .
.
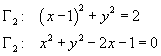
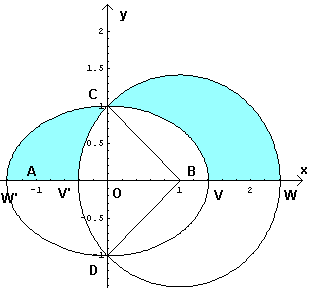
Le intersezioni tra Γ1 e Γ2 si ottengono risolvendo il sistema
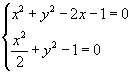
Sottraendo membro a membro si ottiene
![]()
Le intersezioni sono C(0 ; 1) e D(0 ;
-1).
Il coefficiente della retta CB è -1, quello
della retta DB è 1: le due rette sono
perpendicolari, il triangolo CBD è rettangolo in
B.
Il doppio dell'area della regione S si
ottiene sottraendo dalla somma delle aree dell'ellisse e del
cerchio il doppio dell'area della loro intersezione
I. I ha area formata dalla somma di
metà dell'area dell'ellisse con l'area del segmento circolare
CW'DO. A sua volta l'area del segmento circolare
CW'DO può essere ottenuta sottraendo dall'area
di un quarto di cerchio l'area del triangolo
CBD.
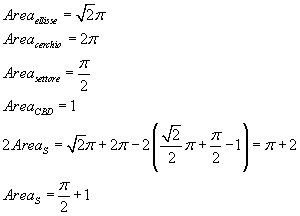
P appartiene al segmento V'W,
quindi
![]()
-
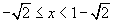
la sezione è un cerchio di raggio
rtale che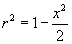
e la funzione è espressa da
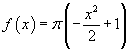
-
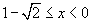
la sezione è una corona circolare compresa tra circonferenza concentriche di raggi
Rertali che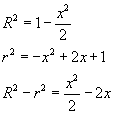
e la funzione è espressa da
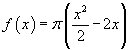
-
la sezione è una corona circolare compresa tra circonferenza concentriche di raggi
Rertali che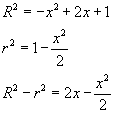
e la funzione è espressa da
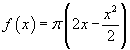
-
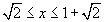
la sezione è un cerchio di raggio
rtale che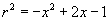
e la funzione è espressa da
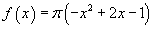
Il grafico è formato da quattro rami di parabole con asse parallelo all'asse delle ordinate.
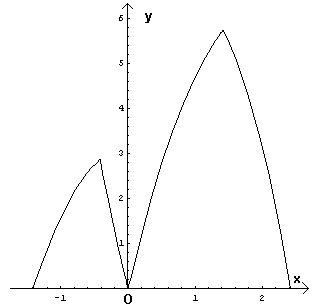
La misura dell'area indicata può essere espressa dall'integrale
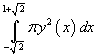
cioè con la misura del volume del solido di rotazione
T.