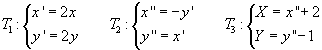
(a cura di Roberto Bigoni)
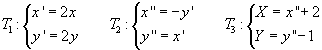
La T1 è una trasformazione lineare di matrice
![]()
cioè una omotetia di centro O.
La T2 è una trasformazione lineare di matrice
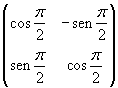
cioè una rotazione di argomento π/2.
La T3 è una traslazione di parametri 2 e -1.
Concatenando le tre trasformazioni si ottiene
![]()
cioè
![]()
Componendo due trasformazioni lineari si ottiene una trasformazione lineare. Componendo poi una trasformazione lineare con una traslazione si ottiene una trasformazione detta affinità. Quindi la T è una affinità.
In generale le affinità trasformano rette in rette e mantengono il parallelismo. Inoltre il rapporto tra le aree di due figure piane corrispondenti in una affinità è uguale al modulo del determinante dell'affinità.
Le traslazioni e le rotazioni sono isometrie, lasciano cioè invariate le lunghezze dei segmenti e le aree delle figure. Le omotetie lasciano invariati gli angoli tra lette ma 'scalano' le lunghezze. In definitiva l'affinità T, data dalla composizione di una omotetia con una rotazione e una traslazione è una similitudine: mantiene gli angoli tra le rette, raddoppia le lunghezze dei segmenti e quadruplica le aree.
Un punto unito si trasforma in se stesso, quindi le sue coordinate si determinano risolvendo il sistema
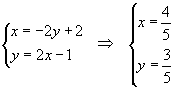
L'affinità T ammette il punto unito U ( 4/5 ; 3/5 ).
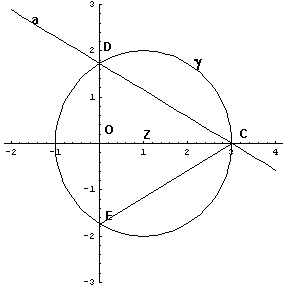
E' immediato dedurre che i punti C, D,
E sono i vertici di un triangolo equilatero il cui
circocentro Z, coincidente con il baricentro, si trova
sulla mediana OC ad un terzo della sua lunghezza: Z
( 1; 0 ).
La circonferenza circoscritta γ ha raggio r =
2.
L'area del segmento circolare S delimitato dalla retta a e dal minore degli archi CD si ottiene facilmente dividendo per tre la differenza tra l'area di γ e l'area del triangolo CDE.
![]()
Ovviamente l'area rimanente S' si ottiene sottraendo dall'area del cerchio l'area del segmento circolare S.
![]()
Poiché, come s'é detto, la similitudine quadruplica le aree, le aree richieste si ottengono moltiplicando per 4 quelle trovate.
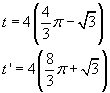
Il segmento CD ha ovviamente misura identica a
quella del segmento DE.
Il minore degli archi CD ha misura pari ad un terzo di
quella della circonferenza, il maggiore ha misura doppia.
I perimetri dei due segmenti circolari sono quindi
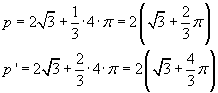
I perimetri delle figure trasformate dalla similitudine sono doppi:
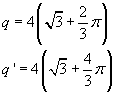
![]()