La funzione, nel punto xo, è positiva e crescente. L'annullamento della derivata
seconda, pur essendo necessario, non è sufficiente ad individuare un punto di flesso, cioè
di un punto (non singolare) che separa due intervalli con concavità di segno diverso.
Perché ci sia un flesso la derivata seconda deve avere segno diverso negli intorni sinistro
e destro del punto, cioè la derivata terza non deve essere nulla. Ma su questa derivata non è
fornita nessuna informazione.
Per determinare i tre esempi richiesti, conviene assumere, come espressioni della derivata seconda, funzioni monomie (nulle per xo=0) ed integrarle due volte, usando le condizioni date sulla derivata prima e sulla funzione per determinare le costanti additive.
Ad esempio, posto f1 ' ' ( x ) = 6 x, segue
![]()
La funzione f1 ( x ) ha un flesso obliquo in xo=0.
Posto f2 ' ' ( x ) = 12 x2, segue
![]()
La funzione f2 ( x ), pur avendo derivata seconda nulla in xo=0, ha concavità positiva negli intorni sinistro e destro di questo punto.
Infine, posto f3 ' ' ( x ) = -12 x2, segue
![]()
La funzione f3 ( x ), pur avendo derivata seconda nulla in xo=0, ha concavità negativa negli intorni sinistro e destro di questo punto.
Perché il grafico di una funzione f ( x ) ammetta in un punto xt tangente parallele alla retta di equazione y = x + 1, bisogna che la derivata della funzione in questo punto sia uguale a 1.
Per tutte e tre le funzioni proposte questa condizione implica xt = 0, quindi, oltre alla retta data, non esistono altre tangenti soddisfacenti alla condizione posta.
La dimostrazione richiesta può essere ottenuta dall'applicazione della derivata logaritmica: da
![]()
applicabile a funzioni ovunque positive, quindi, se la base è positiva, anche a funzioni
f ( x ) = x n.
In questi casi si ottiene immediatamente
![]()
Per x negative - x è positivo, quindi la relazione appena trovata si può applicare a - x:
-
se n è pari, la funzione xn è simmetrica rispetto all'asse delle ordinate e le derivate in due punti opposti sono opposte:
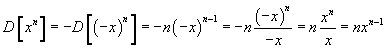
-
se n è dispari, la funzione è simmetrica rispetto all'origine e le derivate in due punti opposti sono uguali:
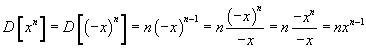
quindi la regola vale anche per basi negative.
Una dimostrazione alternativa si può ottenere applicando il principio di induzione: se una relazione su n vale per n = 1 e vale anche per n + 1, allora vale per ogni n intero.
Se si assume
![]()
si ha che la derivata di x è 1, quindi è vero che D[x1]=1 x0
Si ha inoltre
![]()
quindi la regola di derivazione vale per ogni n intero.