PROBLEMA 2

Nel piano riferito a coordinate cartesiane ortogonali monometriche (x,y) è assegnata la funzione

con a e b diversi da zero.

1. Si trovino i valori di a e b tali che la curva Γ grafico della funzione passi per l'origine degli assi e presenti un minimo assoluto in x=1;
2. si studi e si disegni Γ;
3. si determini, applicando uno dei metodi numerici studiati, un'approssimazione della intersezione positiva di Γ con l'asse x;
4. si determini l'equazione della curva Γ' simmetrica di Γ rispetto alla retta y=y(1);

5. si disegni, per i valori si a e b trovati, il grafico di

   

SOLUZIONE

a)

Il passaggio per l'origine impone

Dato che la funzione, nel suo dominio, è continua e derivabile, il minimo assoluto è anche un minimo relativo; è necessario che per x=1 si annulli la derivata prima

b)

La funzione da studiare è

Il dominio è ]-1; +∞[

Nel dominio la funzione è continua e derivabile.

Per lo studio del segno conviene scrivere

La funzione di sinistra è una parabola con vertice nell'origine e concavità positiva; la funzione di destra è una funzione logaritmica con asintoto verticale x=-1, sempre crescente e passante per l'origine; graficando entrambe le funzioni si vede che si intersecano nell'origine e in un punto di ascissa positiva α.

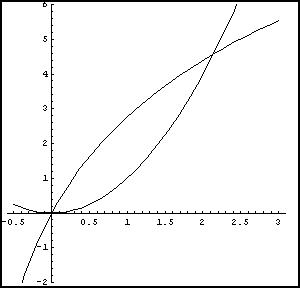
La funzione è positiva in ]-1;0[ U]α; ∞[, negativa in ]0;α[, interseca l'asse delle ascisse nell'origine e nel punto A(α ; 0).

Per x →-1 la f tende a +∞.

La pendenza della funzione è data dal segno della derivata prima

la funzione decresce in ]-1;1[ e cresce in ]1;+ ∞[ con un minimo in M(1;1-4log2 ≈-1,77)

Dato che la funzione per x>1 e sempre crescente e non ammette asintoto orizzontale, per x→ ∞ la funzione diverge.

La concavità è data dal segno della derivata seconda

La derivata seconda è sempre positiva, la concavità è sempre verso l'alto.

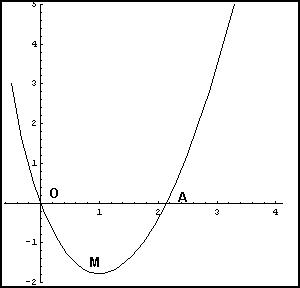
c)

Dal grafico si evince che α è compreso tra 2  e  3;

Con il metodo dicotomico si hanno i valori approssimati

y(2)= - 0,39

y(3)= 3,45

y(2.5)= 1,24

y(2,25)= 0,35

y(2,125)= - 0,04

α è compreso tra 2,125 e 2,250

d)

l’equazione della simmetria è

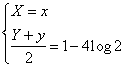
Si ha quindi

Dall’equazione della y si ottiene

e in definitiva

e)

Il grafico del modulo della funzione y si ottiene immediatamente da quello di y 'rovesciando' l'arco negativo

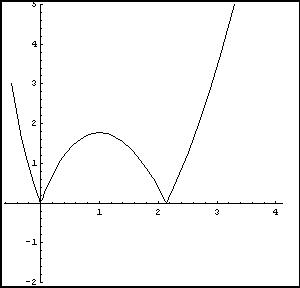
Il modulo ha un massimo relativo per x=1, due punti angolosi nell'origine e in A.