QUESTIONARIO

Provare che una sfera è equivalente ai 2/3 del cilindro circoscritto

Il volume della sfera oltre che per via sintetica può essere ricavato per via analitica come volume generato dalla rotazione di una semicirconferenza attorno al suo diametro.

Scegliendo un sistema di riferimento con origine nel centro e asse delle ascisse dato dalla retta del diametro l'equazione della semicirconferenza di raggio r risulta

il volume di rotazione è dato dall'integrale

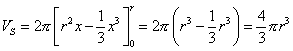
Il cilindro circoscritto ha raggio di base r e altezza 2r. Il suo volume è pertanto

Il rapporto tra i volumi è

Determinare il numero di soluzioni dell'equazione

L'equazione può essere scritta nella forma

e quindi

Le soluzioni dell'equazione sono rappresentate graficamente dalle intersezioni del grafico del coseno iperbolico e dell'iperbole equilatera

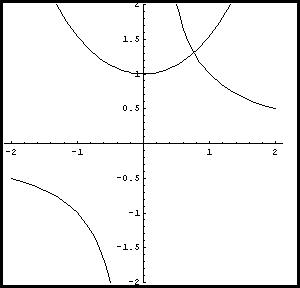
Le curve si incontrano solo in un punto del primo quadrante; l'equazione ammette un'unica soluzione.

Dimostrare che se p(x) è un polinomio, allora tra due qualsiasi radici distinte di p(x) c'è una radice di p'(x).

I polinomi sono funzioni continue e derivabili su tutto R, in particolare in tutti i punti dell'intervallo individuato da due zeri x₁ e x₂ di p(x).  In tale intervallo sono soddisfatti tutti i requisiti del teorema di Rolle e quindi vale la tesi per cui esiste almeno un punto x₀ interno all'intervallo in cui si annulla la derivata prima.

Calcolare la derivata della funzione

Quali conclusioni se ne possono trarre per la f(x)?

La derivata è nulla, la funzione è costante: in particolare per x=0 si ha

e quindi

Calcolare l'integrale

Posto t=log x si ha

Quindi nella variabile t l'integrale diventa

Recuperando la variabile x

Con uno dei metodi di quadratura studiati, si calcoli un'approssimazione dell'integrale definito

e si confronti il risultato ottenuto con il valor esatto dell'integrale.

Il valore esatto dell'integrale è 2.

Poiché l'arco si sinusoide nell'intervallo assegnato ha concavità negativa, il metodo dei trapezi permette di approssimare l'integrale per difetto. La differenza tra il valore esatto e quello approssimato tende a 0 all'aumentare del numero di trapezi considerati.

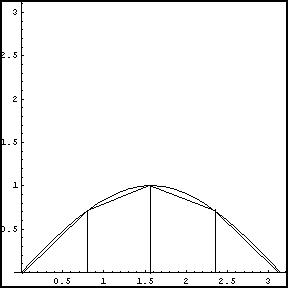
Dividendo per semplicità di calcolo l'intervallo [0,π] in quattro parti uguali, sfruttando la simmetria, la somma delle aree dei trapezi inscritti risulta

Verificato che l'equazione x-e^-x=0 ammette una sola radice positiva compresa tra 0 e 1 se ne calcoli un'approssimazione applicando uno dei metodi numerici studiati.

Scrivendo l'equazione equivalente

e rappresentando le due funzioni nello stesso piano cartesiano

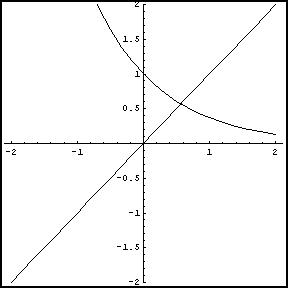
risulta evidente che si intersecano in un unico punto del primo quadrante e quindi l'equazione ammette una sola soluzione.

Usando il metodo di bisezione, per x=0 la funzione

è negativa, mentre per x=1 è positiva.

f(0.5)<0

f(0.75)>0

f(0.625)>0

La soluzione è compresa tra 0.5 e 0.625

Una classe è composta di 12 ragazzi e 4 ragazze.
Tra i sedici allievi se ne scelgono tre a caso: qual è la probabilità che essi siano tutti maschi?

La via più veloce per risolvere il quesito è classificare l'evento come evento composto di tre eventi dipendenti. Quindi

Dire, formalizzando la questione e utilizzando il teorema del valor medio o di Lagrange, se è vero che “se un automobilista compie un viaggio senza soste in cui la velocità media e 60 Km/h, allora almeno una volta durante il viaggio il tachimetro dell'automobile deve indicare esattamente 60 Km/h”.

Supponendo per semplicità un percorso rettilineo, la funzione oraria x(t) è, classicamente, continua e derivabile in qualunque istante del suo dominio. Detti t₁ e t₂  l'istante iniziale e l'istante finale per il teorema di Lagrange esiste almeno un istante t₀ tale che

Il primo membro è la velocità istantanea in t₀, il secondo la velocità media dello spostamento.