Scrivendo la funzione f(x) nella seguente forma
![]()
si osserva che, per x→∞, le frazioni di denominatore ex tendono a 0 e quindi il fattore tra parentesi tende a 1. Dato che il limite di un prodotto è uguale al prodotto dei limiti e che l'esponenziale diverge, si ha
![]()
Per x→-∞ l'esponenziale tende a 0. Scrivendo la funzione f(x) nella seguente forma
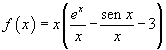
si osserva che le frazioni di denominatore x tendono a 0 e il fattore tra parentesi tende a -3. Si ottiene quindi
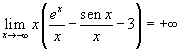
La funzione f(x), somma di funzioni continue su tutto R, è essa pure continua su tutto R. Dato che
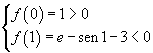
la funzione, per il teorema di Cauchy sulla continuità, deve azzerarsi almeno una volta nell'intervallo [0 ; 1].