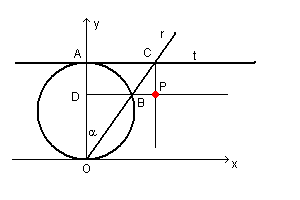
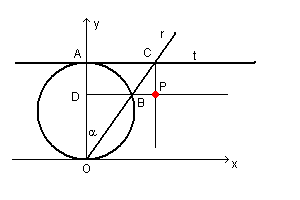
I triangoli rettangoli ODB e OAC sono simili: hanno i cateti proporzionali
OD : DB = OA : AC
AC e DP sono congruenti, quindi
OD : DB = OA : DP
La tangente CA è media proporzionale tra l'intera secante e la sua parte esterna:
OC : AC = AC : BC
AC e DP sono congruenti, quindi
OC : DP = DP : BC
Assumendo il sistema di riferimento della figura e posto
![]()
si ha
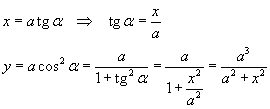
![]()
Per il suo significato geometrico a è positivo.
Il dominio di realtà è R.
Dipendendo solo da x2 la funzione è pari: il suo grafico è simmetrico rispetto
all'asse delle ordinate ed ha un estremo relativo per x=0.
La funzione è sempre positiva e tende a 0 per x→±∞: l'asse delle ascisse è un
asintoto orizzontale del grafico.
Il grafico interseca l'asse delle ordinate nel punto M(0;a).
La derivata prima risulta
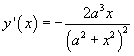
La funzione è crescente per x negative, decrescente per x positive ed ha un massimo assoluto in M.
La derivata seconda risulta
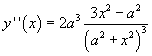
La concavità è positiva in
![]()
negativa in
![]()
Il grafico ha flessi obliqui in
![]()
Grafico
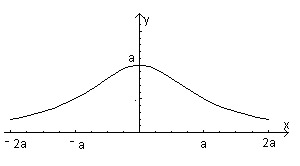
L'area richiesta, data la simmetria della curva, si ottiene dall'integrale
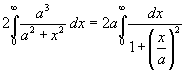
Posto
![]()
si ha
![]()
che è il quadruplo dell'area di un cerchio di raggio a/2.