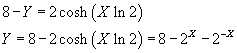![]()
La parità della funzione implica che per ogni x non nullo
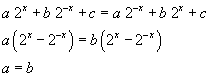
La funzione può quindi essere scritta
![]()
Dato che
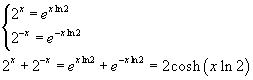
la funzione può anche essere scritta
![]()
Inoltre
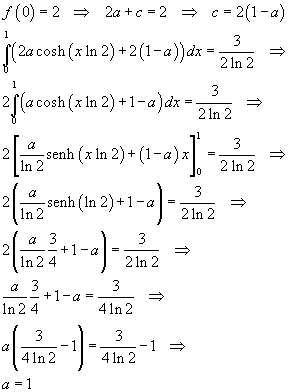
e quindi
![]()
In definitiva g(x) può essere scritta
![]()
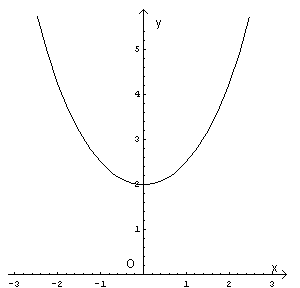
L'espressione di g(x) tramite il coseno iperbolico permette di dedurre subito le caratteristiche del suo grafico: è una catenaria, cioè una curva definita su tutto R, pari, che va all'infinito per x→±∞, con concavità sempre positiva e un minimo assoluto per x=0: M(0;2).
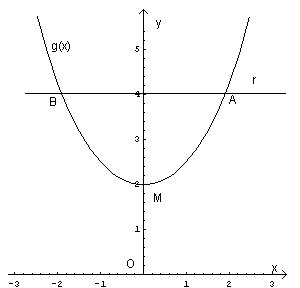
Le ascisse delle intersezioni A e B tra la catenaria e la retta possono essere denotate esattamente risolvendo l'equazione
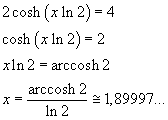
Va considerata anche la soluzione simmetrica x = -arccosh2/ln 2.
Alternativamente si può scrivere l'equazione in notazione esponenziale
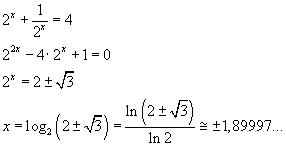
La soluzione positiva può essere approssimata iterativamente con il metodo delle tangenti assumendo come funzione di cui cercare gli zeri
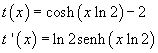
e come termini della successione di approssimazioni
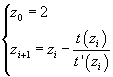
In questo modo si ottiene
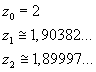
L'area richiesta può essere ottenuta raddoppiando la differenza tra l'area del rettangolo di altezza 4 e base uguale all'ascissa di A e l'area sottesa dall'arco MA di catenaria
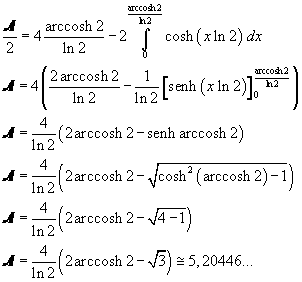
L'integrale richiesto si calcola più agevolmente usando la forma esponenziale di g(x)
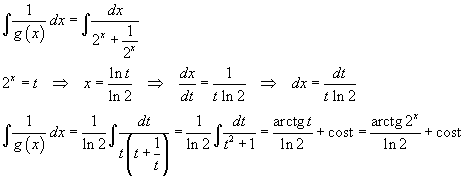
Le equazioni della simmetria rispetto alla retta y=4 sono
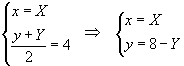
Sostituendo nella funzione g(x) si ha