Il semplice quesito si può risolvere in modo molto elementare, ma per dare l'impressione di saper qualcosa di calcolo combinatorio, conviene inquadrarlo come applicazione del calcolo di disposizioni semplici
![]()
Anche questo semplice quesito appare formulato in modo abbastanza infelice con dati
ridondanti e forse fuorvianti. In base al testo proposto si deve supporre che le scelte
delle scatole siano equiprobabili e quindi ognuna di esse abbia probabilità uguale ad 1/3.
Indicando con P(A), P(B), P(C) le probabilità di estrarre rispettivamente dalle scatole A,
B, C e con P(D|A) la probabilità di estrarre una lampadina difettosa dopo aver scelto la scatola A, ecc.,
la probabilità richiesta P si
ottiene dalla somma
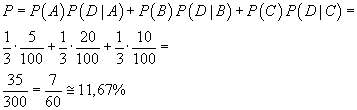
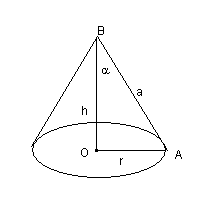
Il volume di un cono è un terzo del prodotto dell'area di base per l'altezza.
![]()
Data l'apotema a, indicando con α l'angolo OBA (0 < α < π/2 ) si ha
![]()
e quindi
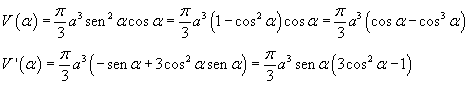
Nel primo quadrante il seno è sempre positivo: per analizzare il segno della derivata prima basta risolvere la disequazione
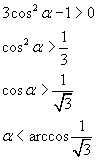
Il volume è massimo quando
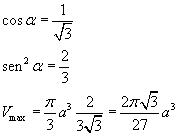
Con a = 2 dm si ha a3 = 8 litri.
![]()
Per risolvere il quesito è sufficiente considerare un qualunque polinomio con quattro zeri reali e poi traslarlo 'alzandolo' di 2 unità. Ad esempio:
![]()
ha zeri in ±1 e ±2. Il polinomio
![]()
soddisfa la richiesta.
I polinomi sono funzioni continue e derivabili su tutto R. Se un polinomio ha almeno due zeri diversi (su questo punto il testo è impreciso), cioè assume lo stesso valore 0 in due punti distinti x1 e x2, allora esiste almeno un punto in ]x1 ; x2[ in cui si annulla la sua derivata prima. Il polinomio della seconda equazione è appunto la derivata prima del polinomio della prima equazione.
Il polinomio p(x)=x3+bx-7 ha derivata prima p ' (x) =3x2+b
Se b è positivo, p ' (x) è sempre positiva, p(x) è sempre crescente ed ha solo uno zero reale. Se b è nullo, p(x) ha come radice reale solo la radice cubica di 7. Dunque è necessario che b sia negativo. Ponendo β = - b, gli estremi relativi di p(x) si hanno per
![]()
Imponendo che gli estremi relativi di p(x) siano discordi si ottiene
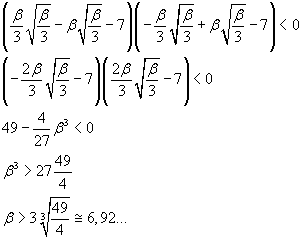
Limitandosi a valori interi di b, rispondono alla richiesta tutti i valori minori di -6.
L'integrale proposto è uno dei più noti in analisi matematica
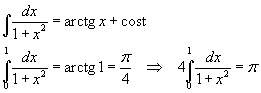
Per approssimarne il valore con la regola dei trapezi, si può suddividere l'intervallo [0 ; 1] in cinque sottointervalli Δx di ampiezza 0,2. Si ottiene
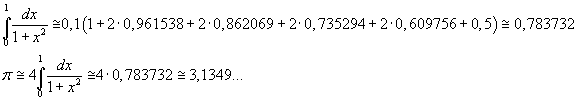
Il volume di rotazione attorno all'asse delle ascisse di un arco di curva f(x), delimitato dai punti di ascissa x1 e x2, è dato dall'integrale
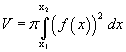
Per rispondere al quesito è quindi sufficiente che il solido richiesto sia quello generato dalla rotazione attorno all'asse delle ascisse dell'arco di curva di equazione
![]()
delimitato dalle ascisse 0 e 1.
La dizione del testo permette comunque anche procedure come la seguente:
Si calcola l'integrale
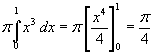
Si propone qualunque solido il cui volume sia quello calcolato: il caso più semplice è il cubo di lato
![]()
Da f ' ' (x) = sen x, integrando, si ottiene f ' (x) = - cos x + k
Utilizzando la condizione al contorno si ottiene
![]()
Quindi
![]()
Integrando la derivata prima si ottiene la f(x)
![]()
Si ha quindi
![]()
Le radici dell'equazione data si possono ottenere graficamente dalle ascisse dei punti di intersezione delle curve di equazioni
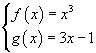
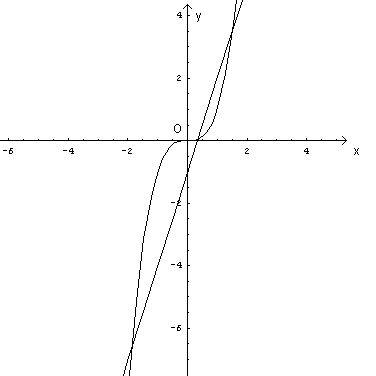
Dal grafico si vede che l'equazione ammette tre radici: x1 in [-3 ; -2], x2 in [0 ; 1], x3 in [1 ; 2].
Per approssimare il valore di x2 si può usare il metodo delle tangenti assumendo come valore iniziale della successione di approssimazioni 0:
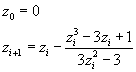
Si ottiene
z0 = 0
z1 = 0,333333...
z2 = 0,347222...
z3 = 0,347296...
z4 = 0,347296...