Y557 - ESAME DI STATO DI LICEO SCIENTIFICO
CORSO SPERIMENTALE-P.N.I.

Tema di MATEMATICA

Il candidato risolva uno dei due problemi e 5 dei 10 quesiti del questionario.

PROBLEMA 1

Sia γ la curva d'equazione:

ove k e λ sono parametri positivi.

1. Si studi e si disegni γ;
2. si determini il rettangolo di area massima che ha un lato sull'asse x e i vertici del lato opposto su γ;
3. sapendo che e assumendo si trovi il valore da attribuire a k affinché l'area compresa tra γ e l'asse x sia 1;
4. per i valori di k e λ sopra attribuiti, γ è detta curva standard degli errori o delle probabilità o normale di Gauss (da Karl Friedrich Gauss, 1777-1855). Una media μ≠0 e uno scarto quadratico medio σ≠1 come modificano l'equazione e il grafico?

PROBLEMA 2

Sia f la funzione così definita:

con a e b numeri reali diversi da zero.

1. Si dimostri che, comunque scelti a e b, esiste sempre un valore di x tale che
2. Si consideri la funzione g ottenuta dalla f ponendo . Si studi g e se ne tracci il grafico.
3. Si consideri per x>0 il primo punto di massimo relativo e se ne fornisca una valutazione approssimata applicando un metodo iterativo a scelta.

svolgimento

QUESTIONARIO

1. La misura degli angoli viene fatta adottando una opportuna unità di misura. Le più comuni sono i gradi sessagesimali, i radianti, i gradi centesimali. Quali ne sono le definizioni?

   svolgimento

   ---

    

2. Si provi che la superficie totale di un cilindro equilatero sta alla superficie della sfera ad esso circoscritta come 3 sta a 4.

   svolgimento

   ---

    

3. Un solido viene trasformato mediante una similitudine di rapporto 3. Come varia il suo volume? Come varia l.area della sua superficie?

   svolgimento

   ---

    

4. Dati gli insiemi A={1,2,3,4} e B={a,b,c} quante sono le applicazioni (le funzioni) di A in B?

   svolgimento

   ---

    

5. Dare un esempio di funzione g, non costante, tale che:

   

   svolgimento

   ---

    

6. Dare un esempio di funzione f(x) con un massimo relativo in (1,3) e un minimo relativo in (-1,2).

   svolgimento

   ---

    

7. Tra i triangoli di base assegnata e di uguale area, dimostrare che quello isoscele ha perimetro minimo.

   svolgimento

   ---

    

8. Si trovino due numeri reali a e b, a≠b, che hanno somma e prodotto uguali.

   svolgimento

   ---

    

9. Si dimostri che l.equazione ammette una e una sola soluzione e se ne calcoli un valore approssimato utilizzando un metodo iterativo a scelta.

   svolgimento

   ---

    

10. Nel piano è data la seguente trasformazione:

    

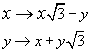
    Di quale trasformazione si tratta?

    
    
    

    svolgimento

     

_______________________________________________________________

Durata massima della prova: 6 ore.
È consentito l’uso della calcolatrice tascabile non programmabile e la consultazione del vocabolario di italiano.
Non è consentito lasciare l’Istituto prima che siano trascorse 3 ore dalla dettatura del tema.