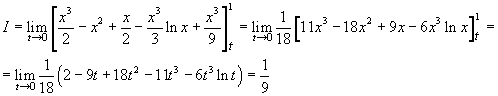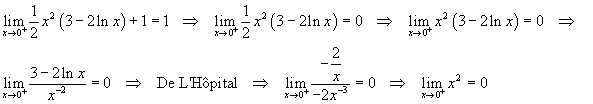
f(x) è definita solo a destra di 0: si può analizzarla solo in un intorno destro.
f(x) è continua da destra di 0 se
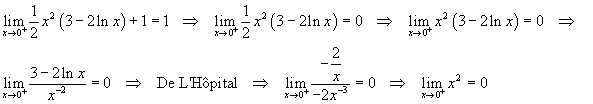
L'ultimo limite è immediato, per cui è dimostrata la continuità da destra.
Il limite da destra della derivata è
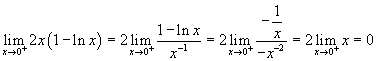
La derivata converge, dunque è dimostrata la derivabilità da destra.
L'equazione f(x)=0, nel dominio x>0, è equivalente a
Graficando nel dominio le curve descritte dai membri destro e sinistro di questa equazione
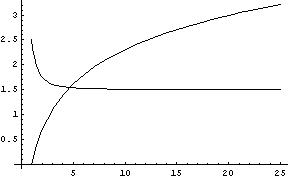
si osserva che il logaritmo è sempre crescente da -∞, mentre l'altra funzione è sempre positiva, sempre decrescente da +∞ e tende asintoticamente a 3/2. Le due curve pertanto si intersecano in un unico punto del I° quadrante. L'equazione ammette una sola soluzione.
Per approssimare la soluzione si può usare il metodo delle tangenti costruendo la successione
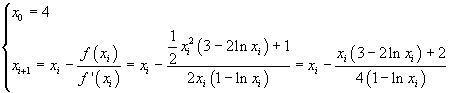
Si ottiene
4 4,91229... 4,70351... 4,69018... 4,69013...
La soluzione cercata xZ è circa 4,69
f(x) è definita reale per x≥0. Dall'analisi precedente si deduce che è positiva per 0≤x<xZ, nulla per x=xZ, negativa per x>xZ.
per x→0 f(x)→1, per x→∞ f(x)→-∞
Per calcolare il limite per x→∞ basta calcolare il limite
e poi, eventualmente, dividerlo per 2 e aggiungere 1. Si ha
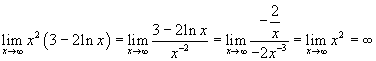
Il punto A(0;1) è un punto d'arresto; in tale punto la derivata da destra è nulla.
Analizzando il segno della derivata prima si ha
La funzione cresce in tale intervallo, decresce oltre e, ha un minimo relativo per xA=0 e un massimo relativo in M
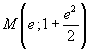
La derivata seconda è 
ed è positiva per xF<1, nulla per
xF=1, negativa oltre. Per tale valore si ha un flesso obliquo
La retta tangente a C in F ha coefficiente angolare dato da f'(1)=2 ed ha quindi equazione
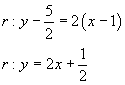
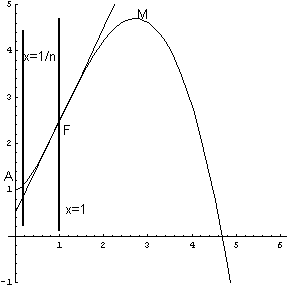
L'area An è data da
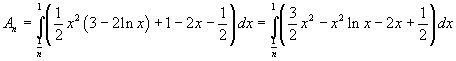
Le primitive dei monomi in x sono immediate. Una primitiva del termine x2lnx si ottiene abbastanza facilmente integrando per parti
Con la regola di Torricelli si ha
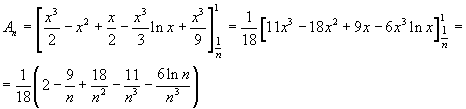
Il limite del rapporto tra logaritmo e cubo si può determinare trattando la n come variabile continua e applicando il teorema di De L'Hôpital. Si ottiene quindi
Questo risultato deve coincidere con il valore dell'integrale da 0 a 1 della differenza tra l'equazione della curva e quella della retta:
