Problema 2

Quesito 1

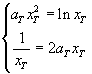
La funzione f(x), definita reale solo per x positivi, è rappresentata graficamente dalla nota curva logaritmica che è sempre crescente, interseca l'asse delle ascisse nel punto di ascissa 1, tende a -∞ per x→0 e a +∞ per x→+∞.

La funzione g(x) è rappresentata graficamente da un fascio di parabole con asse di simmetria coincidente con l'asse delle ordinate e vertice nell'origine. Del fascio fa parte anche la parabola che degenera in retta e coincide con l'asse delle ascisse.

Per a≤0 le parabole intersecano la curva logaritmica in un sol punto e quindi l'equazione ammette una e una sola soluzione.

Per a>0 si possono avere:

• una parabola tangente alla curva logaritmica; sia a_T il parametro che corrisponde alla parabola tangente;
• parabole con parametro a<a_T che intersecano la logaritmica in due punti distinti; si hanno quindi due soluzioni distinte;
• parabole con parametro a>a_T che non intersecano la logaritmica; quindi non ci sono soluzioni reali.

Considerando la parabola per cui si ha tangenza e detto T il punto di tangenza, si ha

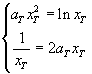
Ricavando a_T dalla seconda equazione e sostituendo nell'altra si ottiene

Quesito 2

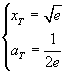
In questo caso l'equazione della parabola è . Questa parabola interseca la retta di equazione y=-1 nel punto I le cui coordinate sono date dalla soluzione del sistema (x>0)

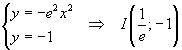
La logaritmica interseca la stessa retta nel punto J le cui coordinate sono date dalla soluzione del sistema (x>0)

I punti I e J coincidono, quindi parabola e logaritmica si intersecano in I.

Il diagramma è il seguente

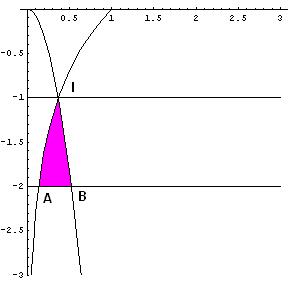
Il calcolo dell'area in colore risulta molto facilitato se si cambia il sistema di riferimento, interpretando l'asse delle ascisse come asse delle ordinate, e il verso negativo dell'asse delle ordinate come verso positivo dell'asse delle ascisse. In questo sistema di riferimento la curva logaritmica è espressa dalla curva esponenziale di equazione , mentre l'equazione della parabola è .

L'area si ottiene quindi calcolando l'integrale

Quesito 3

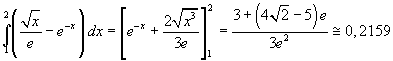
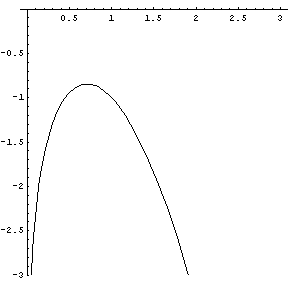
Scegliendo a=1 la funzione h(x) è , definita solo per argomenti positivi e sempre negativa in quanto, come s'è visto al punto 1, per argomenti uguali, la parabola ha ordinate maggiori della logaritmica.

Per x→0, la funzione tende a -∞; per x→∞ il limite, intuitivo, può essere calcolato in questo modo:

La derivata prima è positiva in , dove la funzione cresce, negativa in , dove la funzione cala, e si annulla per . Si ha un massimo in .

La derivata seconda è sempre negativa e quindi la concavità è costantemente negativa e non ci sono flessi.