La funzione assegnata può essere più vantaggiosamente notata come
La derivata prima è
Il dominio di positività della derivata prima è
Se a<1, lna<0, quindi
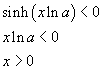
Se a>1, lna>0, quindi
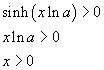
In entrambi i casi, la funzione è crescente per x positive, nulla per x nulla, decrescente per x negative.
Si ha
.
Il coseno iperbolico è definito reale per ogni x reale, è una funzione pari, diverge positivamente per x → ∞, non ha asintoti, è decrescente per x negative, crescente per x positive, ha un minimo assoluto di valore 1 per x=0, concavità sempre positiva. Il grafico della funzione f(x), proporzionale al coseno iperbolico, mantiene lo stesso andamento, con un minimo assoluto di valore 2. Il suo grafico è
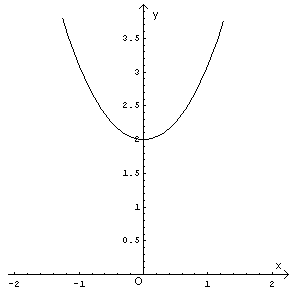
Si pone
Il coseno iperbolico non si annulla mai, dunque la funzione reciproca, nota come secante iperbolica, è definita reale per ogni x, è pari, tende a 0 per x → ∞ e quindi il suo grafico ha un asintoto orizzontale coincidente con l'asse delle ascisse. Lo stesso vale per la funzione s(x).
La s(x) è crescente per x negative, decrescente per x positive e ha un massimo assoluto di valore 1/2 per x=0.
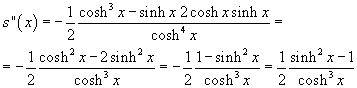
La concavità è positiva nel dominio individuato, negativa per
. Ci sono
flessi obliqui per
.
Per il calcolo dell'ordinata dei flessi, si nota che
, quindi
le ordinate sono
.
Si ottiene il seguente grafico
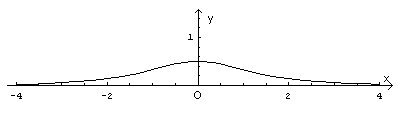
L'integrale risulta facilitato se si adotta l'espressione esponenziale della s(x)
Ponendo
si ha
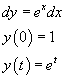
e si ottiene l'integrale equivalente
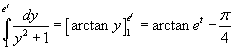
Poiché
,
il limite richiesto è
.
L'area rappresentata in figura vale π/2.
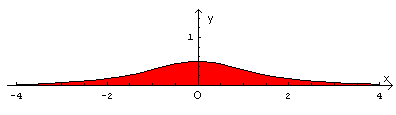
Usando lo sviluppo in serie dell'arcotangente, si può approssimare a piacere, per quanto piuttosto lentamente, il valore richiesto.
