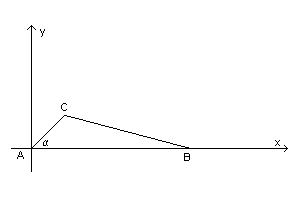
Indicando con α la misura dell'angolo in A, si ha ovviamente
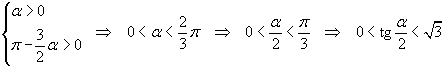
Nel sistema di riferimento cartesiano ortogonale con origine in A e asse delle ascisse coincidente con la retta orientata AB, le equazioni delle rette AC e BC risultano
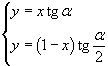
Considerando solo il semipiano delle ordinate positive si ha inoltre
Usando le cosiddette formule parametriche si ha quindi
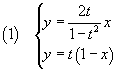
Uguagliando i secondi membri si ottiene x in funzione di t:
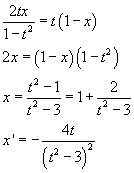
Per valori positivi di t la x è decrescente. Si ha quindi
Ricavando t dalla seconda delle (1) e sostituendo nella prima si ottiene
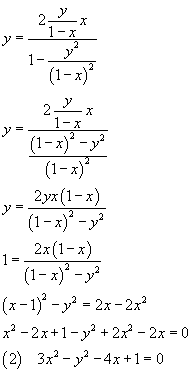
La (2) è una possibile espressione dell'equazione di γ con la limitazione individuata sul dominio delle x.
La (2) può essere scritta
Usando la tecnica del completamento del quadrato si ha
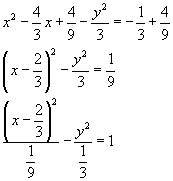
γ è quindi un ramo di iperbole con centro C e semiassi a e b
.
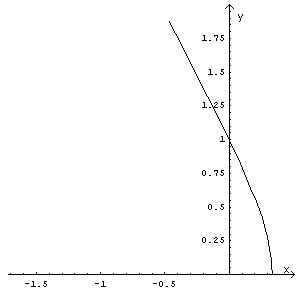
Per ottenere il grafico, conviene disegnare l'iperbole nel suo sistema canonico e poi traslare l'origine di 2/3 verso sinistra. È comunque del tutto accettabile anche la procedura standard di studio della funzione esplicita
Con riferimento alla prima figura, l'altezza relativa al lato AC misura
;
l'altezza relativa al lato BC misura
. La funzione
da massimizzare è quindi
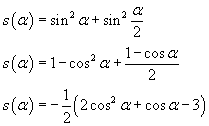
Il massimo si ha, nel dominio ammesso per α, per il valore di α che annulla la derivata prima e rende negativa la derivata seconda. Le derivate sono
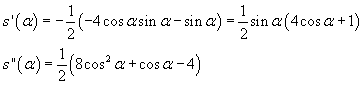
La derivata prima si annulla se
, valore
che rende negativa la derivata seconda. Dunque la funzione ha il suo massimo se
L'angolo in B è la metà di questo valore, cioè circa 52°14'.
Con il valore assegnato per l'angolo ABC, il triangolo è un triangolo aureo: il lato AC è la sezione aurea del lato di misura 1. Quindi la misura di AC è φ.