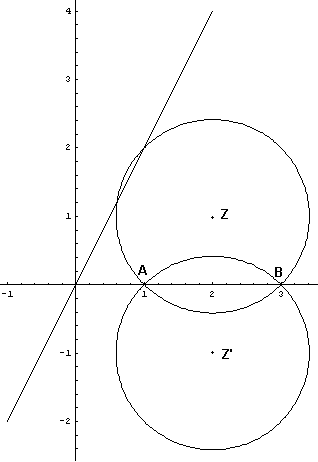
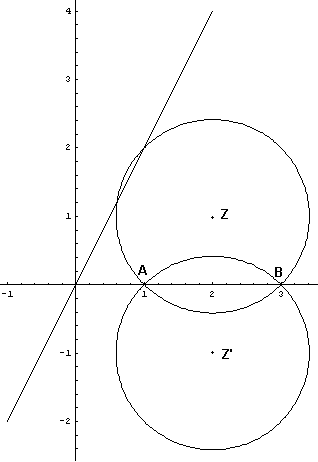
Il luogo dei punti C tali che
![]() è il maggiore degli archi AB della
circonferenza circoscritta ad un quadrato di lato AB. Il raggio di tale circonferenza è
è il maggiore degli archi AB della
circonferenza circoscritta ad un quadrato di lato AB. Il raggio di tale circonferenza è
![]() .
.
Sul segmento AB possono essere costruiti due quadrati, quindi possono esistere due di tali circonferenze con centri
![]() .
.
Le distanze d e d' dei due centri dalla retta y=2x sono
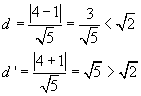
dunque l'unica circonferenza che interseca la retta è quella con centro in Z, di equazione
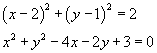
I punti di intersezione della circonferenza con la retta si ottengono risolvendo il sistema
![]()
Si ottiene
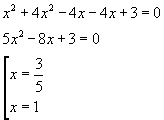
Le coordinate dei punti di intersezione sono quindi quelle dichiarate nel testo.
Indicando con
![]() le coordinate di un punto C sulla retta,
si ha immediatamente che l'equazione di una delle altezze del triangolo ABC è
le coordinate di un punto C sulla retta,
si ha immediatamente che l'equazione di una delle altezze del triangolo ABC è
![]() . Per determinare la posizione
dell'ortocentro si può procedere nel seguente modo.
. Per determinare la posizione
dell'ortocentro si può procedere nel seguente modo.
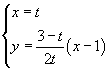
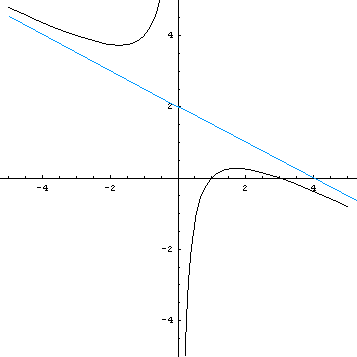
Grafico di γ
![]()
La funzione è crescente in
![]() ,
decrescente in
,
decrescente in
![]() ,
ha un minimo relativo in
,
ha un minimo relativo in
![]() e un massimo relativo in
e un massimo relativo in
![]()
![]()
La concavità è positiva per x negative e viceversa. Non ci sono flessi.
I coefficienti angolari delle tangenti a γ nei punti A e B sono dati dai valori della derivata per le ascisse corrispondenti.
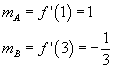
Le equazioni delle tangenti sono
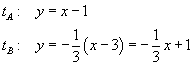
Sottraendo membro a membro si ha
![]()
Le tangenti si intersecano nel punto ![]()
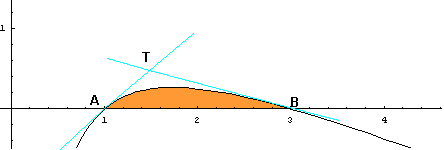
L'area Ω si può ottenere sottraendo dall'area del triangolo ABT l'area sottesa all'arco AB di γ.
![]()
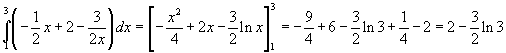
![]()
Per il calcolo approssimato del logaritmo si può usare il seguente sviluppo in serie deducibile dalla Serie di Mercatore
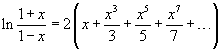
![]()
![]()
Arrestando il calcolo al terzo addendo, già minore di un centesimo, si ha
![]()