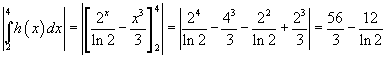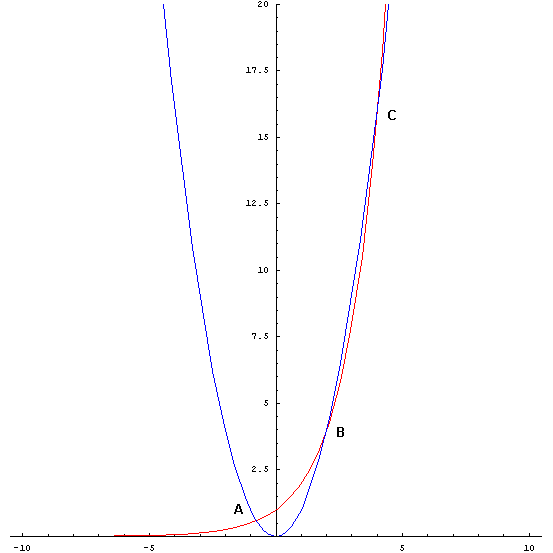
La f(x) è un'esponenziale di base maggiore di 1: è sempre crescente, diverge positivamente per x→∞, tende a 0 per x→-∞, interseca l'asse delle ordinate nel punto (0;1)
La g(x) è una parabola con vertice nell'origine e diverge positivamente per x→±∞.
Per x=2 e x=4 le due funzioni assumono entrambe lo stesso valore cioè 4 in un caso e 16 nell'altro, per cui i due grafici si intersecano nei punti B(2;4) e C(4;16).

Per approssimare l'ascissa di A si può usare il metodo delle tangenti applicato all'approssimazione degli zeri della funzione h(x)=2x-x2 assumendo
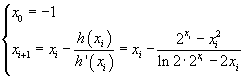
Si ottiene la seguente successione

Gli zeri di h(x)=2x-x2 sono xA, approssimato nel quesito precedente, xB=2 e xC=4.
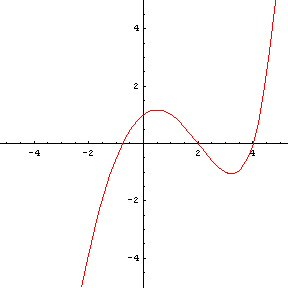
h(x) è definita per ogni x reale, è negativa per x<xA, positiva per xA<x<xB, negativa per xB<x<xC, positiva per x>xC. Diverge negativamente per x→-∞, positivamente per x→+∞.
Il segno della derivata prima si può stimare graficando insieme le curve di equazioni f(x) e
![]() .
.
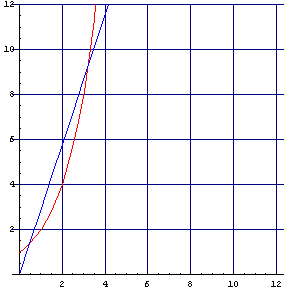
La funzione è crescente da -∞ fino a circa x=0.5, decrescente da qui fino a circa x=3 e quindi decrescente.
![]() : c'è un flesso per
x∼2.
: c'è un flesso per
x∼2.
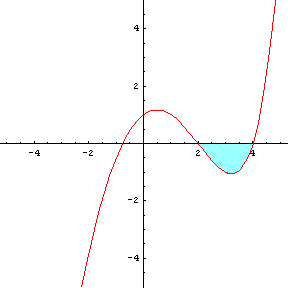
L'area richiesta è data da