Poiché f è data dal prodotto di un polinomio per una esponenziale, f è continua e derivabile infinite volte su tutto R.
La derivata del polinomio
![]() è
è
![]()
Dunque
![]()
La derivata di f è quindi
![]()
Poiché esponenziali e fattoriali sono sempre positivi, la derivata prima è positiva per
![]() .
.
Se n è pari:
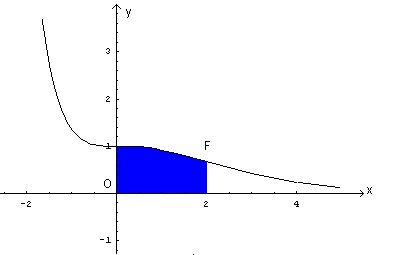
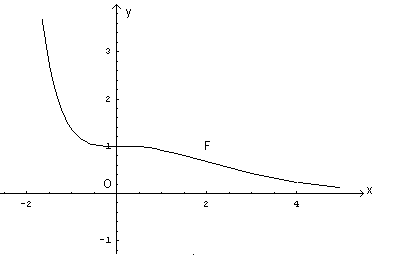
La funzione g è espressa da
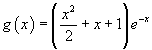
Per quanto precedentemente osservato, g è continua su tutto R e sempre decrescente. Il trinomio tra parentesi ha discriminante negativo, dunque è sempre positivo. Anche l'esponenziale è sempre positiva. Il loro prodotto è sempre positivo, quindi la funzione è positiva in tutto il dominio. Si ha inoltre
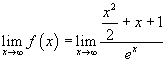
Applicando ripetutamente il teorema di De L'Hôpital si trova che tale limite vale 0. Dunque la g ha l'asse delle ascisse come asintoto orizzontale.
Le derivate prima e seconda sono
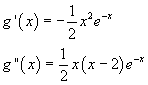
Si ha
![]()
Per x→∞ il coefficiente angolare della tangente diverge: non c'è asintoto obliquo.
La derivata seconda è positiva per valori esterni all'intervallo [0;2]. Quindi la concavità è positiva in
]-∞;0[ e ]2;+∞[e negativa in ]0;2[. Per x=0 si ha il flesso orizzontale già individuato e per
x = 2 un flesso obliquo ![]() .
.
Per calcolo dell'integrale si applica due volte il metodo dell'integrazione per parti:
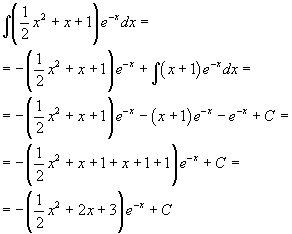
quindi
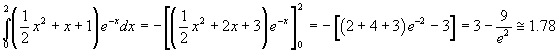
Il valore calcolato rappresenta l'area compresa tra l'arco di curva con estremi di ascisse 0 e 2 e l'asse delle ascisse.