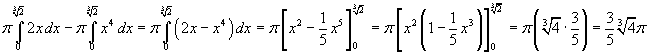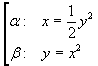
Parabole
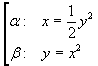
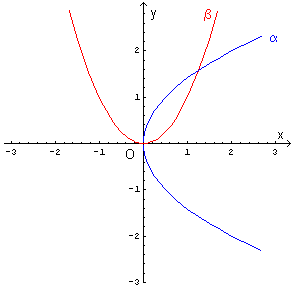
La parabola α ha vertice nell'origine, asse di simmetria coincidente con l'asse delle ascisse e concavità
rivolta verso destra. Il suo fuoco ha ascissa
, ordinata 0 e direttrice di equazione
.
La parabola β ha vertice nell'origine, asse di simmetria coincidente con l'asse delle ordinate e concavità
rivolta verso l'alto. Il suo fuoco ha ordinata
, ascissa 0 e direttrice di equazione
.
Le coordinate del punto A si determinano risolvendo il sistema
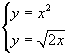
per x>0 e risultano
.
Il calcolo della radice cubica di 2 rimanda al noto problema dell'antica geometria greca, noto come problema della duplicazione del cubo o problema di Delo. La geometria greca ammetteva solo quelle procedure che noi oggi chiamiamo 'con riga e compasso' e questo problema, assieme a quello della quadratura del cerchio e della trisezione dell'angolo si dimostrato insolubile con tali procedure.
L'approssimazione della radice cubica di 2 può essere ottenuta con il metodo delle tangenti applicato
alla soluzione dell'equazione
.
Assumendo
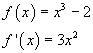
si ha
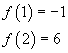
Per teorema di continuità di Bolzano, lo zero dell'equazione è compreso tra 1 e 2. Si ottiene quindi
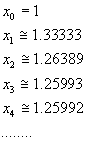
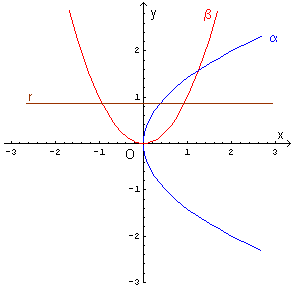
Una retta r di equazione
ha intersezione di ascissa positiva con la parabola β per
e intersezione con la
parabola α per
.
La distanza tra i due punti di intersezione risulta
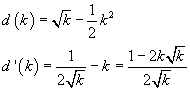
Per k>0 la derivata prima è positiva per
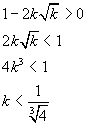
Si ha quindi il segmento di lunghezza massima per la retta
Le sezioni del solido W sono corone circolari le cui circonferenze hanno raggi di misure rispettivamente
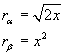
Il volume di W può essere ottenuto sottraendo dal solido prodotto dalla rotazione dell'arco di α il solido prodotto dalla rotazione dell'arco di β.
