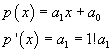
Si può dimostrare l'asserzione proposta applicando il Principio di Induzione Matematica.
L'asserzione è vera se p(x) è di primo grado. Infatti in questo caso
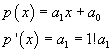
Assumendo valida l'asserzione si ha che la derivata di ordine n+1 di p(x) è uguale a 0.
Inoltre un polinomio P di grado n+1 risulterà di forma
La sua derivata prima è
La derivata di ordine n di P'(x) coincide con la derivata di ordine n+1 di P(x) e, in virtù dell'asserzione, risulta
Dunque l'asserzione è valida per ogni n naturale.
Assumendo un sistema di riferimento cartesiano ortogonale tridimensionale Axyz con origine in A, asse x sovrapposto al lato AB, asse y sovrapposto al lato AC e asse z perpendicolare al piano del triangolo per A, siano b la lunghezza del lato AB, c la lunghezza del lato AC e p la quota di P. Rappresentando gli spigoli del tetraedro ABCP con vettori applicati all'origine si ha
Gli spigoli AB e BP sono perpendicolari, cioè il triangolo ABP, come è ovvio, è retto in B.
In modo analogo si dimostra che il triangolo PCB è retto in B.
Il prodotto scalare di AC per AP risulta
AP e AC sono perpendicolari, quindi il triangolo PAC è retto in A.
L'ascissa x del punto T di tangenza deve essere tale che
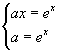
La tangenza si ha quindi per x=1. Le coordinate di T sono quindi T(0;e) e il coefficiente angolare della retta è quindi uguale alla costante di Eulero e.
L'angolo che la retta forma con il verso positivo dell'asse x è
La derivata prima della funzione proposta risulta
e, per qualunque valore non nullo di x è positiva. Per x=0 la derivata diverge positivamente: si ha un flesso a tangente verticale.
La funzione è continua e sempre non decrescente e il suo valore varia da meno infinito a più infinito. Dunque il suo diagramma interseca l'asse delle ascisse in un solo punto. In particolare si ha
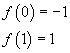
Per il teorema di continuità di Bolzano, lo zero è compreso tra 0 e 1.
Applicando l'algoritmo delle tangenti si ottiene
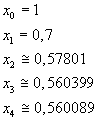
Perché il diagramma G di una funzione f sia simmetrico rispetto alla retta di equazione x=k bisogna che, indicando con d una variabile non negativa, sia
Ponendo
si ottiene
Ponendo
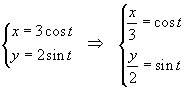
ed elevando entrambi i membri al quadrato si ottiene
cioè l'equazione canonica di un'ellisse di semiassi a=3 e b=2.
Assumendo che la probabilità di nascere maschio o femmina siano uguali e indipendenti dalle nascite precedenti, la probabilità chiesta è banalmente 0,5.
Il problema proposto è del tutto analogo a chiedersi qual è la probabilità che, dopo aver lanciato una moneta e avere avuto croce, un secondo lancio dia ancora croce.
(N.d.R. : non si capisce il senso di questo quesito in una prova di esame nazionale.)
Poiché i tre coefficienti binomiali sono in progressione aritmetica, il secondo è la media aritmetica tra il primo e il terzo.
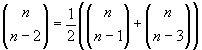
Sviluppando in fattoriali e con successive semplificazioni si ottiene
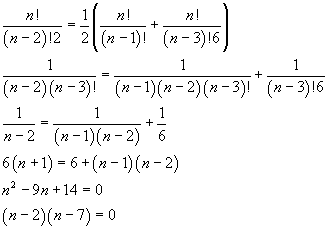
L'unica soluzione accettabile è n=7.
Se l'angolo in B misura 45°, il minimo valore possibile per il lato AC si ha con un angolo retto
in C, quindi è
. Se AC misura 2, risulta
'troppo corto' per chiudere il triangolo.
Se invece l'angolo in B misura 30°, la minima misura di AC risulta
. In questo caso il lato AC
di misura 2, può chiudere il triangolo formando in C o un angolo acuto γ o un angolo ottuso supplementare
di γ.
Il volume del solido generato dalla rotazione dell'arco di curva considerato attorno all'asse x è
quindi la risposta a) è errata.
Il volume del solido generato dalla rotazione dell'arco di curva considerato attorno all'asse y è
quindi la risposta b) è errata.
Il solido di base R le cui sezioni siano semicerchi di raggio
ha volume
e quindi anche la risposta c) è errata.
In definitiva nessuna delle congetture proposte è valida.